1. Heap이란?
Heap은 heap property를 만족하는 complete binary tree이다.
(1) complete binary tree
binary tree는 자식 노드가 2개만 존재하며, 오른쪽 자식과 왼쪽 자식이 구분되는 tree이다.
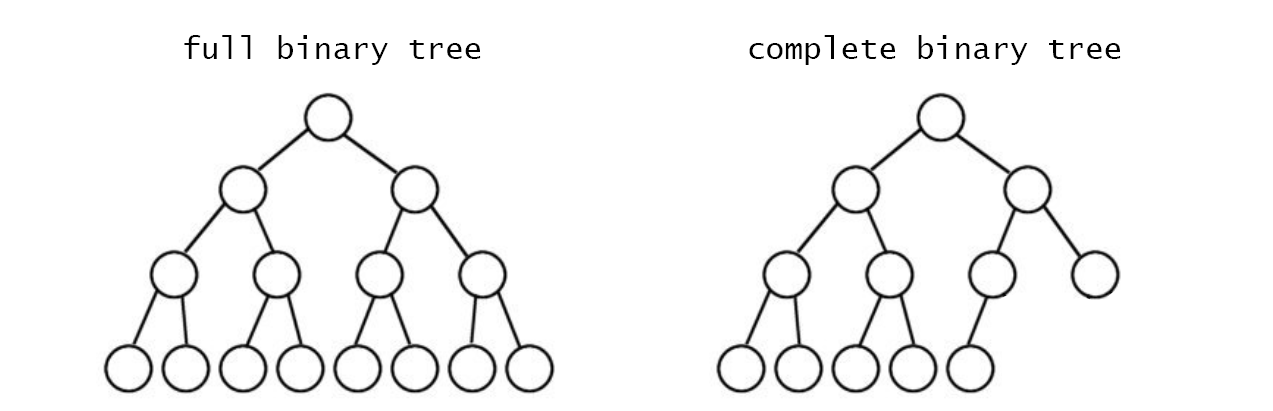
- full binary tree: 모든 층(level)의 노드들이 꽉 차있는 형태
- complete binary tree: 마지막 층(level)을 제외한 층의 노드들은 꽉 차 있으며, 마지막 층의 오른쪽부터 몇개의 노드가 비어있을 수 있음
(2) heap property
이 글에서는 max-heap property를 기준으로 다루고자 한다.
- max-heap property: 부모는 자식보다 크거나 같다
- min-heap property: 부모는 자식보다 작거나 같다
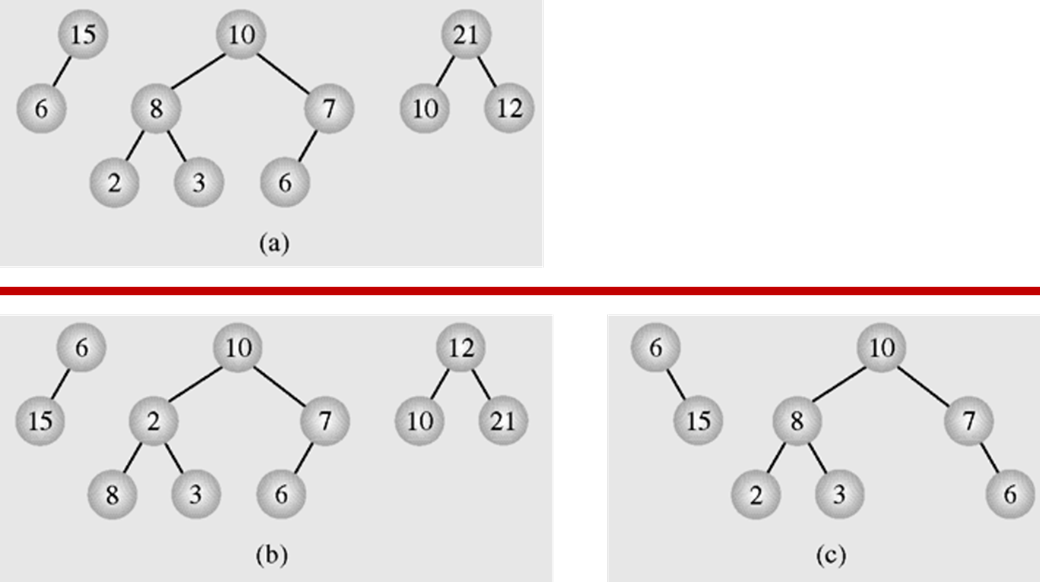
(3) 배열을 통한 Heap의 표현
Heap은 일차원 배열로 표현이 가능하다. 배열의 index를 $[1,2 \cdots n]$이라 할때
- 루트 노드: $A[1]$
- $A[i]$의 부모: $A[\frac{i}{2}]$
- $A[i]$의 왼쪽 자식: $A[2i]$
- $A[i]$의 오른쪽 자식: $A[2i+1]$
2. Heapify
Heap Sort의 핵심은 Max-Heapify이다. Max-Heapify는 Heap의 모든 노드들의 부모, 자식이 max-heap property를 만족하도록 만드는 과정이다.
핵심은 두 자식들 중 더 큰 쪽이 나보다 크면 교환하는 과정을 반복적으로 수행하는 것이다.
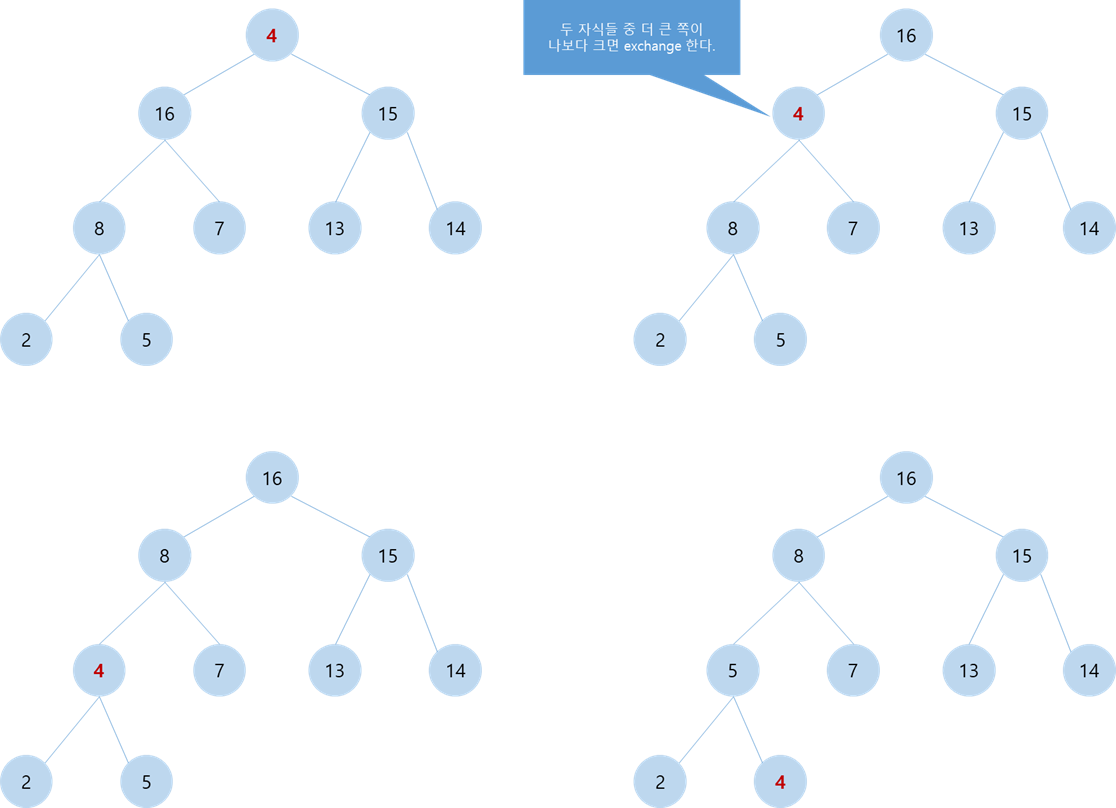
Heap, Heapify 과정에 대해서 알아보았다. 다음 글에서 Heap Sort에 대해서 알아보도록 하겠다.
[References]
- 권오흠 교수, 알고리즘(강의 링크)
'알고리즘' 카테고리의 다른 글
| [3. 검색트리] 이진트리 검색 (2) (0) | 2021.04.03 |
|---|---|
| [3. 검색트리] 이진트리 검색 (1) (0) | 2021.04.03 |
| [2. 정렬] 분할정복법(Divide and Conquer) (0) | 2021.03.15 |
| [2. 정렬] 기본적인 정렬 알고리즘 (0) | 2021.03.09 |
| [1. 순환(Recursion)] 순환 알고리즘 설계 (0) | 2021.03.06 |
1. Heap이란?
Heap은 heap property를 만족하는 complete binary tree이다.
(1) complete binary tree
binary tree는 자식 노드가 2개만 존재하며, 오른쪽 자식과 왼쪽 자식이 구분되는 tree이다.

- full binary tree: 모든 층(level)의 노드들이 꽉 차있는 형태
- complete binary tree: 마지막 층(level)을 제외한 층의 노드들은 꽉 차 있으며, 마지막 층의 오른쪽부터 몇개의 노드가 비어있을 수 있음
(2) heap property
이 글에서는 max-heap property를 기준으로 다루고자 한다.
- max-heap property: 부모는 자식보다 크거나 같다
- min-heap property: 부모는 자식보다 작거나 같다

(3) 배열을 통한 Heap의 표현
Heap은 일차원 배열로 표현이 가능하다. 배열의 index를
- 루트 노드:
2. Heapify
Heap Sort의 핵심은 Max-Heapify이다. Max-Heapify는 Heap의 모든 노드들의 부모, 자식이 max-heap property를 만족하도록 만드는 과정이다.
핵심은 두 자식들 중 더 큰 쪽이 나보다 크면 교환하는 과정을 반복적으로 수행하는 것이다.

Heap, Heapify 과정에 대해서 알아보았다. 다음 글에서 Heap Sort에 대해서 알아보도록 하겠다.
[References]
- 권오흠 교수, 알고리즘(강의 링크)
'알고리즘' 카테고리의 다른 글
| [3. 검색트리] 이진트리 검색 (2) (0) | 2021.04.03 |
|---|---|
| [3. 검색트리] 이진트리 검색 (1) (0) | 2021.04.03 |
| [2. 정렬] 분할정복법(Divide and Conquer) (0) | 2021.03.15 |
| [2. 정렬] 기본적인 정렬 알고리즘 (0) | 2021.03.09 |
| [1. 순환(Recursion)] 순환 알고리즘 설계 (0) | 2021.03.06 |
