이전 글에서 Heap Sort를 위해 필요한 Heap, Heapify 개념을 다루었다.
Heap Sort는 배열이 주어졌을 때 다음과 같은 과정을 통해 정렬한다.
① 주어진 배열로 Max Heap을 만든다.
② Max Heapl에서 최대값(루트)를 가장 마지막 값과 바꾼다. (이때 가장 마지막 값은 정렬이 된 것이므로 힙의 일부가 아닌 것으로 간주함)
③ 루트노드에 대해서 Max-Heapify한다
④ 남은 노드가 1개가 될 때 까지 ②,③을 반복한다
크게 생각한다면 Max Heap을 만들고(초기화), iterative하게 Max-Heapify하는 과정을 통해 배열을 정렬하는 것이다.
1. Heap Sort 과정
(1) Max Heap 만들기
정렬되지 않는 배열을 추상적으로 complete binary tree로 표현하고, max-heap property를 만족하도록 배열의 원소들을 배치하는 과정이다.
i. 먼저 배열이 주어진다면 그대로 complete binary tree로 표현할 수 있다.
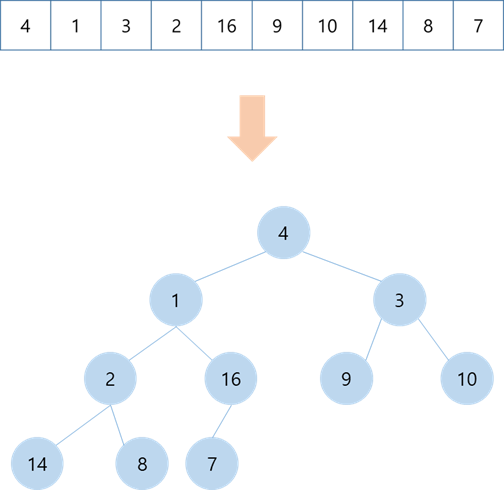
ii. 이후, 마지막 이전의 층(level)의 노드들 중 맨 오른쪽에서부터 볼때 자식 노드가 있는 첫번째 노드부터 순차적으로 max heap property를 만족(Max-Heapify)하도록 원소들을 배열한다. (무슨 말인지 모르겠는데,, 아래 그림을 보자)
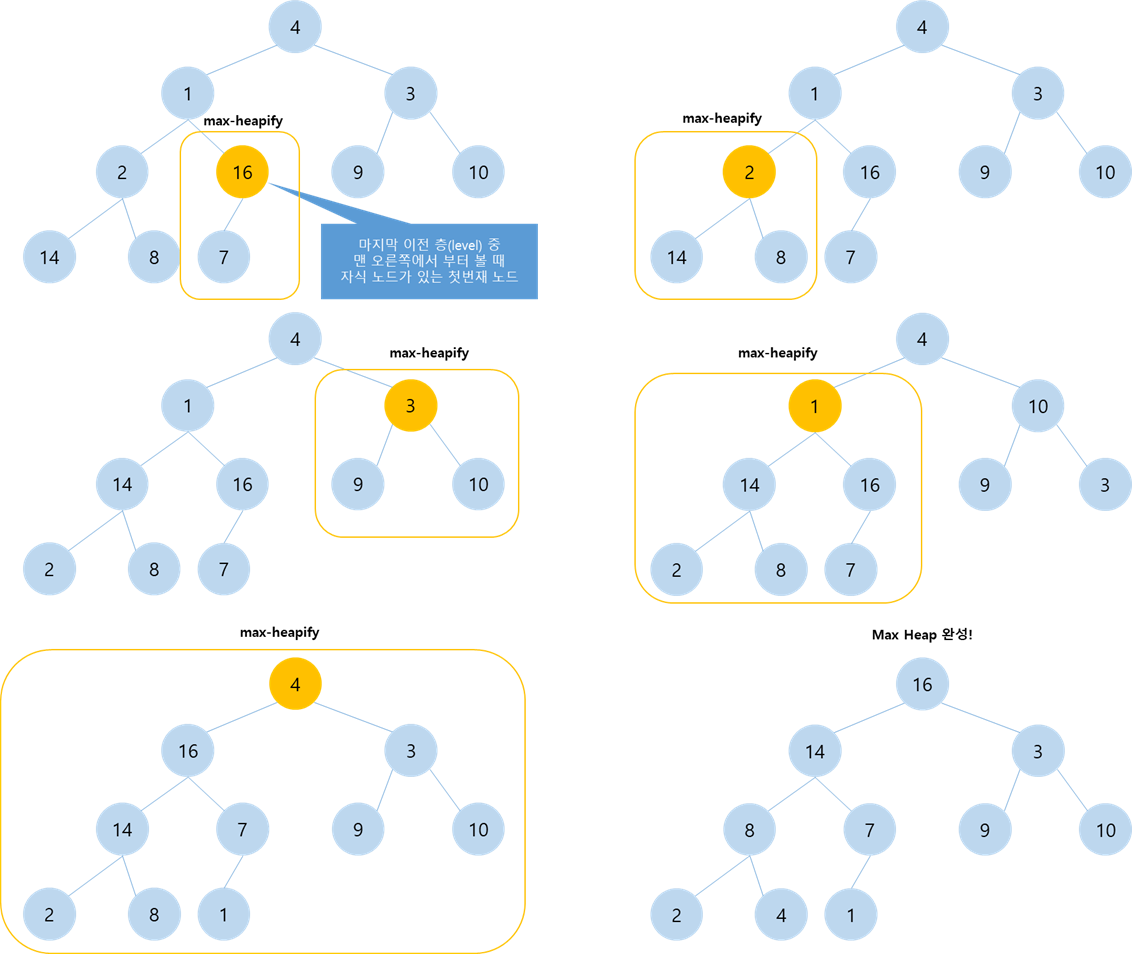
그림에서 표현하자면 위와 같은 순서로 Max-Heapify하게 되는데, 배열에서 보자면 딱 중간에 위치한 값부터 하나씩 역행하며 Max-Heapify하는 과정이다(2로 나눈 몫 index 부터)
(2) Iterative Max-Heapify
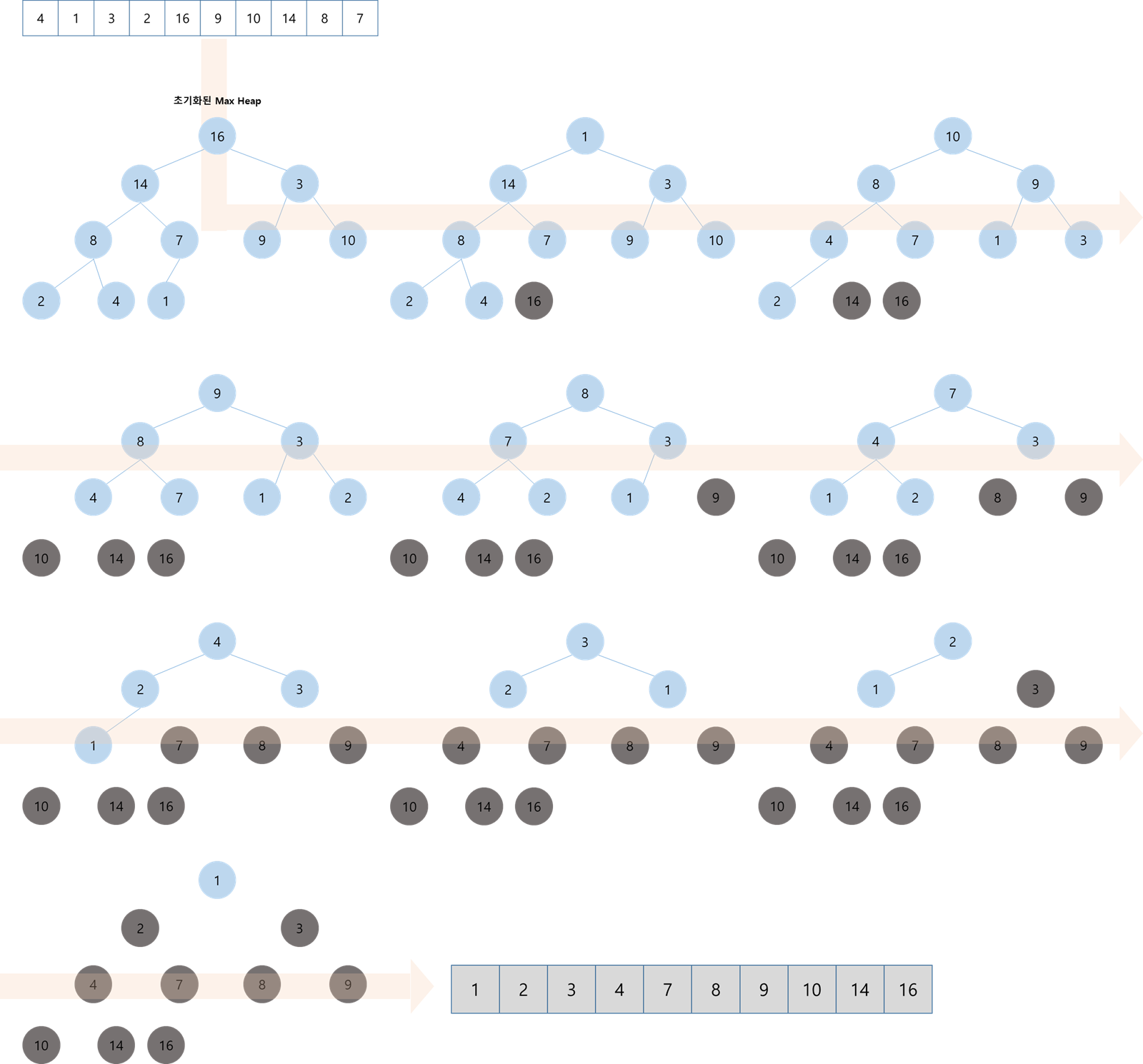
초기화된 Max-Heap complete binary tree를 통해 정렬된 배열을 얻는 과정이다. Max-Heap complete binary tree가 주어졌을 때 root 노드는 해당 tree에서 최대값이며, 배열상으로는 첫번째에 위치하게 된다. 이 값을 배열의 마지막 위치로 옮기고, 해당 값을 제외한 배열에 대해서 Max-Heapify를 수행한다. 이 과정을 아래 그림과 같이 반복적으로 수행하여 가장 큰 값들이 순차적으로 배열 뒤쪽에 쌓이면서 정렬된 배열을 얻을 수 있다.
2. Heap Sort 시간 복잡도
앞서 얘기한 것 처럼 Heap Sort는 (1)Max Heap을 만들고(초기화) (2)iterative하게 Max-Heapify하는 과정으로 진행된다. (1)의 경우 시간 복잡도가 $O(n)$이고 (2)의 경우 complete binary tree의 층 수($log(n)$) 만큼 Max-Heapify하는 과정($n$)이므로 시간복잡도가 $O(nlog(n))$이다.
'알고리즘' 카테고리의 다른 글
| [3. 검색트리] 이진트리 검색 (2) (0) | 2021.04.03 |
|---|---|
| [3. 검색트리] 이진트리 검색 (1) (0) | 2021.04.03 |
| [2. 정렬] Heap Sort (1) (0) | 2021.04.01 |
| [2. 정렬] 분할정복법(Divide and Conquer) (0) | 2021.03.15 |
| [2. 정렬] 기본적인 정렬 알고리즘 (0) | 2021.03.09 |
이전 글에서 Heap Sort를 위해 필요한 Heap, Heapify 개념을 다루었다.
Heap Sort는 배열이 주어졌을 때 다음과 같은 과정을 통해 정렬한다.
① 주어진 배열로 Max Heap을 만든다.
② Max Heapl에서 최대값(루트)를 가장 마지막 값과 바꾼다. (이때 가장 마지막 값은 정렬이 된 것이므로 힙의 일부가 아닌 것으로 간주함)
③ 루트노드에 대해서 Max-Heapify한다
④ 남은 노드가 1개가 될 때 까지 ②,③을 반복한다
크게 생각한다면 Max Heap을 만들고(초기화), iterative하게 Max-Heapify하는 과정을 통해 배열을 정렬하는 것이다.
1. Heap Sort 과정
(1) Max Heap 만들기
정렬되지 않는 배열을 추상적으로 complete binary tree로 표현하고, max-heap property를 만족하도록 배열의 원소들을 배치하는 과정이다.
i. 먼저 배열이 주어진다면 그대로 complete binary tree로 표현할 수 있다.

ii. 이후, 마지막 이전의 층(level)의 노드들 중 맨 오른쪽에서부터 볼때 자식 노드가 있는 첫번째 노드부터 순차적으로 max heap property를 만족(Max-Heapify)하도록 원소들을 배열한다. (무슨 말인지 모르겠는데,, 아래 그림을 보자)

그림에서 표현하자면 위와 같은 순서로 Max-Heapify하게 되는데, 배열에서 보자면 딱 중간에 위치한 값부터 하나씩 역행하며 Max-Heapify하는 과정이다(2로 나눈 몫 index 부터)
(2) Iterative Max-Heapify
초기화된 Max-Heap complete binary tree를 통해 정렬된 배열을 얻는 과정이다. Max-Heap complete binary tree가 주어졌을 때 root 노드는 해당 tree에서 최대값이며, 배열상으로는 첫번째에 위치하게 된다. 이 값을 배열의 마지막 위치로 옮기고, 해당 값을 제외한 배열에 대해서 Max-Heapify를 수행한다. 이 과정을 아래 그림과 같이 반복적으로 수행하여 가장 큰 값들이 순차적으로 배열 뒤쪽에 쌓이면서 정렬된 배열을 얻을 수 있다.

2. Heap Sort 시간 복잡도
앞서 얘기한 것 처럼 Heap Sort는 (1)Max Heap을 만들고(초기화) (2)iterative하게 Max-Heapify하는 과정으로 진행된다. (1)의 경우 시간 복잡도가 $O(n)$이고 (2)의 경우 complete binary tree의 층 수($log(n)$) 만큼 Max-Heapify하는 과정($n$)이므로 시간복잡도가 $O(nlog(n))$이다.
'알고리즘' 카테고리의 다른 글
| [3. 검색트리] 이진트리 검색 (2) (0) | 2021.04.03 |
|---|---|
| [3. 검색트리] 이진트리 검색 (1) (0) | 2021.04.03 |
| [2. 정렬] Heap Sort (1) (0) | 2021.04.01 |
| [2. 정렬] 분할정복법(Divide and Conquer) (0) | 2021.03.15 |
| [2. 정렬] 기본적인 정렬 알고리즘 (0) | 2021.03.09 |
