기존 Transformer 기반 모델(BERT, GPT 등..) 보다 훨씬 더 긴 sequence 데이터를 입력으로 받을 수 있는 연구가 공개되어 정리하고자 합니다. 논문은 글의 제목이며 여기서 확인할 수 있습니다.
0. 핵심 아이디어: Graph Sparcification
본 연구의 핵심 아이디어 sparse random graph이며, 다음과 같은 흐름으로 연구되었습니다.
- self-attention → fully-connected graph: self-attention을 각 token들의 linking으로 본다면 fully-connected graph로 표현할 수 있음
- fully-connected graph → sparse random graph: self-attention graph를 훨씬 더 크게, 그리고 sparse하게 만들면 훨씬 더 긴 sequence를 처리할 수 있으며 성능을 유지할 수 있음
1. Introduction
self-attention은 Transormer 논문에서 소개되었습니다. 다음과 같은 장점 때문에 매우 혁신적이라고 평가되었었습니다.
- Self-attention mechanism은 parallel하게 계산할 수 있어 연상량을 높임. Self-attention 자체의 성능적 우수성도 연구결과를 통해 입증됨
- RNN 모델 등에서 문제가 되는 sequential dependency를 해결함
Transormer 모델은 연산량이 길이의 제곱에 비례하기 때문에 input sequence 길이에 제한을 둡니다. 보통 512 token으로 많이 하는데, 대부분의 문헌의 특성상 corpus 자체의 크기는 매우 크지만 context의 길이 분포가 exponential 하기 때문에 사용하기에 큰 문제가 되지 않았떤 것이죠. 하지만 512 token보다 훨씬 긴 sequence에 대해서는 효과적이지 못하기 때문에 추가 연구가 많이 진행되었었습니다.
(1) sequence 길이가 제한된 모델을 여러번 사용(sliding window): 문서를 쪼개서 모델에 여러번 입력하여 output을 cocantenate하여 사용하거나, 긴 문서에서 관련있는 부분만 찾는데 사용
(2) full attention을 탈피하고자 하는 연구들: masking 길이를 늘리거나 global token 수를 늘림
저자들은 다음과 같은 아이디어를 기반으로 Transformer 기반의 long sequence를 연구했습니다.
- Self-attention에서 inner-product를 적게 사용하며 full self-attention 성능을 달성할 수는 없을까?
- sparse attention mechanism이 원래 모델의 expressivity(e.g. contextualized embeding), flexibility(e.g. 다양한 downstream task에 적용)를 유지할 수 있을까?
- Graph Sparsification에 착안해서 full self-attention을 sparse하게 만들어보자
그리고 Big Bird 모델에 대한 개요는 다음과 같습니다.
- 기존 모델들 보다 8배 더 긴 sequence input을 다룰 수 있음(4096 tokens)
- random attention, window attention, global attention으로 구성된 sparse attention mechanism 적용(★)
2. Big Bird Architecture
BigBird는 Transformer architecture를 기반으로 합니다. 즉 multi-head self-attention과 feed-forward network로 구성된 layer를 여러겹 쌓아서 만든 구조이며, 다만 self-attention layer에서 full-attention이 아닌 sparse attention으로 연산하는 것이 차이점입니다.

Big Bird 모델의 핵심인 generalized attention mechanism에 대해 설명드리겠습니다. 먼저 $d$ 차원으로 embedding된 $n$개의 input sequence$X=(x_{1}, \cdots , x_{n}) \in R^{n \times d}$ 가 주어집니다. 이때 generalized attention mechanism은 노드(vertex) 모든 token $[n] = {1, \cdots n}$이고 엣지가 attention mechanism이 수행되는 set of inner-product인 유향 그래프(directed graph) $D$로 표현할 수 있습니다.

결과를 먼저 설명하자면 $i$ 번째 token에 대한 generalized attention mechanism output vector는 다음과 같습니다.
$$\begin{align} ATTN_{D}(X)_{i} = x_{i}+\sum_{h=1}^{H}\sigma(Q_{h}(x_{i})K_{h}(X_{N_{i}}))^{T}) \cdot{V_{h}(X_{N_{(i)}})} \tag{1} \end{align} $$
- $N_{i}$: set of out-neighbors of node $i$(out-neighbor: directed graph에서 node $i$가 가리키는 node들)
- $Q_{h}, K_{h}(R^{d} \rightarrow R^{m})$: query & key function, token embedding $x_{i} \in R^{d}$를 $R^{m}$ 차원으로 mapping해주는 함수
- $V_{h}(R^{d} \rightarrow R^{d})$: value function, token embedding $x_{i} \in R^{d}$를 $R^{d}$ 차원으로 mapping해주는 함수
- $\sigma$: scoring function(e.g. softmax, hardmax)
- $H$: head 개수
- $X_{N_{(i)}}$:모든 input token이 아닌 $\{x_{j}: j \in N_{(i)}\}$에 해당하는 token embedding만 쌓아서 만든 matrix
예를 들어 어떤 인접행렬이 0,1로만 이루어져있고, query $i$가 key $j$에 attend하면 1, 아니면 0을 의미한다고 할 때($A \in [0,1]^{n \times n}$), BERT와 같은 full self-attention mechanism을 인접행렬로 표현하면 전부 1로 채워진 인접행렬로 표현이 됩니다. 이렇게 self-attention을 fully-connected graph로 나타낼 수 있으니 graph sparsification 이론을 적용해서 complexity를 낮출 수가 있게됩니다.
기존의 연구에 따르면 random graph를 확장시켜 complete graph의 여러 특징들(e.g. spectral property)을 근사시킬 수 있다고 합니다. 본 연구에서는 sparse random graph for attention mechanism에 반영한 두 가지 성질을 밝히고 있습니다.
(1) Small average path length between nodes
Complete graph에서 edge들이 특정 확률에 의해 남겨진 random graph를 생각해봅시다. 이때 두 노드의 최단 경로(shortest path)는 node의 개수에 logarithmic하게 비례한다는 것이 밝혀져 있습니다. 즉, random graph의 크기를 키우고 sparse하게 만들어도 shortest path가 기하급수적으로 급격히 증가하는 것이 아니고 매우 천천히 변하게 됩니다. 또한 이러한 random graph가 complete graph의 spectral property를 근사하게 되며 second eigenvalue가 first eigenvalue와 차이가 크기 때문에 해당 그래프 위에서의 random walk mixing time이 매우 빨라진다고 합니다.
본 연구에서는 이러한 성질을 각 query가 $r$개의 random key를 attend하는 구조로 반영하였습니다.(그림1-a)
(2) Notion of locality
두번째 insight는 대부분의 자연어 context와 computational biology에서 등장하는 특징인 locality of reference입니다. 즉 어떤 token의 정보는 대부분 주변 token의 정보에서 얻어지고, 멀리 떨어진 token에서 얻게 되는 정보량은 적다는 것입니다. Graph 이론을 적용해보면 locality를 계산하기 위한 방법으로 clustering coefficient(군집 계수)를 활용할 수 있습니다. 예를 들어, 어떤 그래프가 많은 clique, near-clique을 담고 있다면 clustering coefficient가 높습니다.
본 연구에서는 각 node(token)이 window size $w$으로 양옆 단어를 attend 하는 구조를 적용했습니다. 즉, self-attention시 $i$에 위치한 query는 $[i - w/2, i+w/2]$의 key들을 attend하게 됩니다.($A(i, i-w/2:i+w/2)=1$)
하지만 위 구조들을 적용한 self-attention으로는 기존 BERT의 성능이 나오지 않았다고 합니다. 그리고 저자들은 많은 실험과 이론 분석을 통해 global token의 중요성을 파악하고 이를 적극 활용했다고 합니다. 본 연구에서는 두 가지 방법으로 적용했습니다.
- BigBird-ITC(Internal Transformer Construction): 언어 corpus에 존재하는 token 중 특정 몇개를 global token으로 지정하여 모든 token들에 대해 attention 계산
- BigBird-ETC(Extended Transformer Construction): sequence에 $g$개의 global token을 추가(e.g. [CLS])
정리하자면 BigBird의 attention mechanism은 그림1-d와 같이 3가지 attention으로 구성됩니다.
- random attention: query와 $r$개의 random keys간의 attention
- window attention: query 양옆 $w$개의 keys와의 attention
- global attention: query와 $g$개의 global token들과의 attention
3. Theoretical Results about Sparse Attention Mechanism
Section 3는 sparse attention mechanism이 full-attention mechanism과 같이 좋은 이유를 이론적으로 탐색하는 내용을 담고 있습니다. Sparse attention mechanism 기반의 encoder가 Universal Approximator인 점, sparse encoder-decoder transformer가 Turing Complete인 점, 그리고 sparse attetion을 적용할 시 모델의 크기가 증가한다는 점들을 다루고 있습니다.
4. Experiments: Natural Language Processing
Section 4는 input을 사용한 실험 내용을 담고 있습니다. 먼저 MLM(Masked Language Modeling)이 긴 sequence에 대해서도 좋은 contextual representation을 담아낼 수 있는지 확인해보고, Big Bird를 QA와 document classification task에 적용하여 효과성을 보이는 내용을 담고 있습니다.
(1) Encoder
Sparse attention mechanism을 적용한 transformer encoder의 성능에 대한 내용입니다.
i. Pretraining and MLM
기존 BERT pretraining과 똑같이 수행하였으며, 다만 문서의 최대 길이가 512 token에서 4096 token으로 증가했습니다. Blocking, Sparsity 구조의 효율성 덕분에 16gb 메모리에서 batch size 32~64로 실험을 할 수 있었다고 합니다.

ii. Question Answering(QA)
Natural Question, HotpotQA, TriviaQA, WikiHop 데이터셋에 대해 실험을 수행했고 RoBERTa, Longformer보다 좋은 성능을 내는 것을 확인할 수 있습니다.

iii. Classification
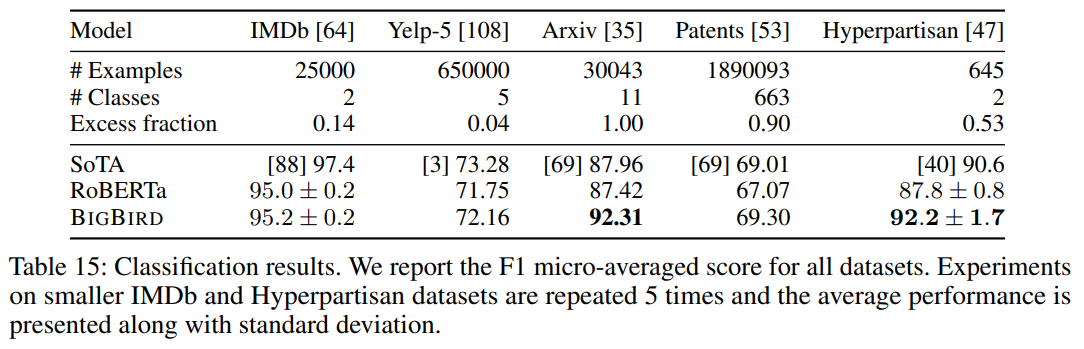
문서 분류 task를 위해 GLUE 뿐만 아니라 다양한 길이와 내용을 담고 있는 데이터셋에 대해서 실험을 수행하였습니다. 그 결과 길이가 더 길면서 학습 데이터가 적은 경우에 큰 성능 향상을 보였다고 합니다(Arxiv dataset에서 5%).

(2) Encoder-Decoder
Decoder를 붙여 실험을 수행한 내용입니다. 본 연구에서는 encoder에만 sparse attetion을 적용하고 decoder는 원래 모델처럼 full attetion을 사용했습니다. 그 이유는 대부분의 상황에서 output sequence는 input sequence보다 작기 때문입니다.
i. Summarization
abstractive summarization 데이터셋에서 long document, short document 모두에 대해 성능을 측정했습니다. Abstractive를 선택한 이유는 긴 문서의 경우 중요한 정보가 고르게 분포가 되어있기 때문에 긴 문서에 대한 요약 성능이 BigBird의 효과성을 보이기에 적절하기 때문입니다. 실험 결과 모든 데이터셋에서 SOTA를 달성했습니다. 또한 길이가 짧은 문서에 대해서도 기존의 SOTA 모델과 비슷한 수준의 성능을 내는 것으로 보아 긴 문서, 짧은 문서에 모두 효과적인 것을 알 수 있습니다.


T5를 만들어낸 구글의 하드웨어 성능을 생각해본다면 BigBird 이후에도 긴 문서를 처리할 수 있는 방법들이 지속적으로 개발될 것 같습니다.
Implementation detail은 다음 페이지에서 다루도록 하겠습니다.
'논문 및 개념 정리' 카테고리의 다른 글
| [2018] Deep contextualized word representations(ELMo) (0) | 2021.03.15 |
|---|---|
| [2017] Attention is All you Need (0) | 2021.03.15 |
| Big Bird Implementation details (0) | 2021.02.16 |
| Exploring Transfer Learning with T5 : the Text-To-Text Transfer Transformer (2) (0) | 2020.06.04 |
| Exploring Transfer Learning with T5 : the Text-To-Text Transfer Transformer (1) (0) | 2020.06.01 |
기존 Transformer 기반 모델(BERT, GPT 등..) 보다 훨씬 더 긴 sequence 데이터를 입력으로 받을 수 있는 연구가 공개되어 정리하고자 합니다. 논문은 글의 제목이며 여기서 확인할 수 있습니다.
0. 핵심 아이디어: Graph Sparcification
본 연구의 핵심 아이디어 sparse random graph이며, 다음과 같은 흐름으로 연구되었습니다.
- self-attention → fully-connected graph: self-attention을 각 token들의 linking으로 본다면 fully-connected graph로 표현할 수 있음
- fully-connected graph → sparse random graph: self-attention graph를 훨씬 더 크게, 그리고 sparse하게 만들면 훨씬 더 긴 sequence를 처리할 수 있으며 성능을 유지할 수 있음
1. Introduction
self-attention은 Transormer 논문에서 소개되었습니다. 다음과 같은 장점 때문에 매우 혁신적이라고 평가되었었습니다.
- Self-attention mechanism은 parallel하게 계산할 수 있어 연상량을 높임. Self-attention 자체의 성능적 우수성도 연구결과를 통해 입증됨
- RNN 모델 등에서 문제가 되는 sequential dependency를 해결함
Transormer 모델은 연산량이 길이의 제곱에 비례하기 때문에 input sequence 길이에 제한을 둡니다. 보통 512 token으로 많이 하는데, 대부분의 문헌의 특성상 corpus 자체의 크기는 매우 크지만 context의 길이 분포가 exponential 하기 때문에 사용하기에 큰 문제가 되지 않았떤 것이죠. 하지만 512 token보다 훨씬 긴 sequence에 대해서는 효과적이지 못하기 때문에 추가 연구가 많이 진행되었었습니다.
(1) sequence 길이가 제한된 모델을 여러번 사용(sliding window): 문서를 쪼개서 모델에 여러번 입력하여 output을 cocantenate하여 사용하거나, 긴 문서에서 관련있는 부분만 찾는데 사용
(2) full attention을 탈피하고자 하는 연구들: masking 길이를 늘리거나 global token 수를 늘림
저자들은 다음과 같은 아이디어를 기반으로 Transformer 기반의 long sequence를 연구했습니다.
- Self-attention에서 inner-product를 적게 사용하며 full self-attention 성능을 달성할 수는 없을까?
- sparse attention mechanism이 원래 모델의 expressivity(e.g. contextualized embeding), flexibility(e.g. 다양한 downstream task에 적용)를 유지할 수 있을까?
- Graph Sparsification에 착안해서 full self-attention을 sparse하게 만들어보자
그리고 Big Bird 모델에 대한 개요는 다음과 같습니다.
- 기존 모델들 보다 8배 더 긴 sequence input을 다룰 수 있음(4096 tokens)
- random attention, window attention, global attention으로 구성된 sparse attention mechanism 적용(★)
2. Big Bird Architecture
BigBird는 Transformer architecture를 기반으로 합니다. 즉 multi-head self-attention과 feed-forward network로 구성된 layer를 여러겹 쌓아서 만든 구조이며, 다만 self-attention layer에서 full-attention이 아닌 sparse attention으로 연산하는 것이 차이점입니다.

Big Bird 모델의 핵심인 generalized attention mechanism에 대해 설명드리겠습니다. 먼저

결과를 먼저 설명하자면
예를 들어 어떤 인접행렬이 0,1로만 이루어져있고, query
기존의 연구에 따르면 random graph를 확장시켜 complete graph의 여러 특징들(e.g. spectral property)을 근사시킬 수 있다고 합니다. 본 연구에서는 sparse random graph for attention mechanism에 반영한 두 가지 성질을 밝히고 있습니다.
(1) Small average path length between nodes
Complete graph에서 edge들이 특정 확률에 의해 남겨진 random graph를 생각해봅시다. 이때 두 노드의 최단 경로(shortest path)는 node의 개수에 logarithmic하게 비례한다는 것이 밝혀져 있습니다. 즉, random graph의 크기를 키우고 sparse하게 만들어도 shortest path가 기하급수적으로 급격히 증가하는 것이 아니고 매우 천천히 변하게 됩니다. 또한 이러한 random graph가 complete graph의 spectral property를 근사하게 되며 second eigenvalue가 first eigenvalue와 차이가 크기 때문에 해당 그래프 위에서의 random walk mixing time이 매우 빨라진다고 합니다.
본 연구에서는 이러한 성질을 각 query가
(2) Notion of locality
두번째 insight는 대부분의 자연어 context와 computational biology에서 등장하는 특징인 locality of reference입니다. 즉 어떤 token의 정보는 대부분 주변 token의 정보에서 얻어지고, 멀리 떨어진 token에서 얻게 되는 정보량은 적다는 것입니다. Graph 이론을 적용해보면 locality를 계산하기 위한 방법으로 clustering coefficient(군집 계수)를 활용할 수 있습니다. 예를 들어, 어떤 그래프가 많은 clique, near-clique을 담고 있다면 clustering coefficient가 높습니다.
본 연구에서는 각 node(token)이 window size
하지만 위 구조들을 적용한 self-attention으로는 기존 BERT의 성능이 나오지 않았다고 합니다. 그리고 저자들은 많은 실험과 이론 분석을 통해 global token의 중요성을 파악하고 이를 적극 활용했다고 합니다. 본 연구에서는 두 가지 방법으로 적용했습니다.
- BigBird-ITC(Internal Transformer Construction): 언어 corpus에 존재하는 token 중 특정 몇개를 global token으로 지정하여 모든 token들에 대해 attention 계산
- BigBird-ETC(Extended Transformer Construction): sequence에
정리하자면 BigBird의 attention mechanism은 그림1-d와 같이 3가지 attention으로 구성됩니다.
- random attention: query와
- window attention: query 양옆
- global attention: query와
3. Theoretical Results about Sparse Attention Mechanism
Section 3는 sparse attention mechanism이 full-attention mechanism과 같이 좋은 이유를 이론적으로 탐색하는 내용을 담고 있습니다. Sparse attention mechanism 기반의 encoder가 Universal Approximator인 점, sparse encoder-decoder transformer가 Turing Complete인 점, 그리고 sparse attetion을 적용할 시 모델의 크기가 증가한다는 점들을 다루고 있습니다.
4. Experiments: Natural Language Processing
Section 4는 input을 사용한 실험 내용을 담고 있습니다. 먼저 MLM(Masked Language Modeling)이 긴 sequence에 대해서도 좋은 contextual representation을 담아낼 수 있는지 확인해보고, Big Bird를 QA와 document classification task에 적용하여 효과성을 보이는 내용을 담고 있습니다.
(1) Encoder
Sparse attention mechanism을 적용한 transformer encoder의 성능에 대한 내용입니다.
i. Pretraining and MLM
기존 BERT pretraining과 똑같이 수행하였으며, 다만 문서의 최대 길이가 512 token에서 4096 token으로 증가했습니다. Blocking, Sparsity 구조의 효율성 덕분에 16gb 메모리에서 batch size 32~64로 실험을 할 수 있었다고 합니다.

ii. Question Answering(QA)
Natural Question, HotpotQA, TriviaQA, WikiHop 데이터셋에 대해 실험을 수행했고 RoBERTa, Longformer보다 좋은 성능을 내는 것을 확인할 수 있습니다.

iii. Classification
문서 분류 task를 위해 GLUE 뿐만 아니라 다양한 길이와 내용을 담고 있는 데이터셋에 대해서 실험을 수행하였습니다. 그 결과 길이가 더 길면서 학습 데이터가 적은 경우에 큰 성능 향상을 보였다고 합니다(Arxiv dataset에서 5%).


(2) Encoder-Decoder
Decoder를 붙여 실험을 수행한 내용입니다. 본 연구에서는 encoder에만 sparse attetion을 적용하고 decoder는 원래 모델처럼 full attetion을 사용했습니다. 그 이유는 대부분의 상황에서 output sequence는 input sequence보다 작기 때문입니다.
i. Summarization
abstractive summarization 데이터셋에서 long document, short document 모두에 대해 성능을 측정했습니다. Abstractive를 선택한 이유는 긴 문서의 경우 중요한 정보가 고르게 분포가 되어있기 때문에 긴 문서에 대한 요약 성능이 BigBird의 효과성을 보이기에 적절하기 때문입니다. 실험 결과 모든 데이터셋에서 SOTA를 달성했습니다. 또한 길이가 짧은 문서에 대해서도 기존의 SOTA 모델과 비슷한 수준의 성능을 내는 것으로 보아 긴 문서, 짧은 문서에 모두 효과적인 것을 알 수 있습니다.


T5를 만들어낸 구글의 하드웨어 성능을 생각해본다면 BigBird 이후에도 긴 문서를 처리할 수 있는 방법들이 지속적으로 개발될 것 같습니다.
Implementation detail은 다음 페이지에서 다루도록 하겠습니다.
'논문 및 개념 정리' 카테고리의 다른 글
| [2018] Deep contextualized word representations(ELMo) (0) | 2021.03.15 |
|---|---|
| [2017] Attention is All you Need (0) | 2021.03.15 |
| Big Bird Implementation details (0) | 2021.02.16 |
| Exploring Transfer Learning with T5 : the Text-To-Text Transfer Transformer (2) (0) | 2020.06.04 |
| Exploring Transfer Learning with T5 : the Text-To-Text Transfer Transformer (1) (0) | 2020.06.01 |
