한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다. GMM 내용은 여기와 여기를 많이 참고하였다.
앞선 글에서 비모수적(non-parametric) 클러스터링 알고리즘 종류들을 살펴보았다. 이 글에서는 모수적(parameter) 클러스터링의 대표적인 방법인 GMM을 살표보고자 한다.
1. GMM(Gaussian Mixture Model)
GMM은 혼합가우시안 모델로 여러개의 Gaussian 분포를 선형결합해서 만든 분포라는 뜻이다. 실제 현실에서의 복잡한 데이터 분포를 설명할 때 적합하다. 아래와 같은 데이터는 하나의 Gaussian 분포로는 설명이 어렵기 때문에 여러개를 합쳐서 표현할 수 있다.

1) GMM 수식
먼저 Gaussian Distribution(Normal Distribution)은 다음과 같이 표현된다.
$$N(x; \mu, \Sigma) = \frac{1}{(2\pi)^{D/2}\left| \Sigma \right|^{1/2}}\text{exp}\left[ -\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu) \right]$$
K개의 Gaussian Distribution을 선형결합한 GMM superposition(중첩)은 다음과 같이 표현할 수 있으며 이를 Gaussian Mixture라고 부른다.
$$p(x) = \sum_{k=1}^{K}\pi_{k}N(x|\mu_{k}, \Sigma_{k})$$
- $\mu_{k}$: Mean
- $\Sigma_{k}$: Covariance matrix
- $\pi_{k}$: mixing coefficient($\sum_{k=1}^{K}\pi_{k}=1, \ 0 \le \pi_{k} \lt 1$)
각각의 Gaussian은 각자의 $\mu_{k}, \Sigma_{k}$를 가지고 있으며, $\pi_{k}$는 각 Gaussian의 weight을 의미하며 K개 Gaussian들을 weighted sum으로 계산하여 Gaussian density를 계산하게 된다.
GMM이 parametric estimation인 이유는 아래 세 가지 parameter에 의해 결정되기 때문이며, 주어진 데이터셋으로 아래 파라미터를 추정하는 것을 GMM을 학습시키는 것이라 한다.
$$\begin{array}{}
\theta = \{\pi, \mu, \Sigma \} \\
\pi = \{ \pi_{1}, \cdots, \pi_{K} \}, \ \mu = \{ \mu_{1}, \cdots, \mu_{K} \}, \ \Sigma = \{ \Sigma_{1}, \cdots, \Sigma_{K} \} \\
\end{array}$$
2) GMM을 활용한 분류와 responsibility(책임값)
먼저 GMM학습이 완료되어 클러스터링이 가능하다고 할때, 주어진 데이터 $x_{n}$이 속한 클러스터를 찾는 것은 어느 Gaussian 분포에서 생성되었는지를 찾는 것이다. 먼저 이를 표현하기 위한 확률값인 responsibitiliy $\gamma(z_{nk})$를 다음과 같이 정의한다.
$$\gamma(z_{nk}) = p(z_{nk}=1|x_{n})$$
위 식에서 $z_{nk} \in {0,1}$은 어떤 데이터 $x_{n}$이 주어졌을 때 GMM의 $k$번째 Gaussian이 해당 데이터가 속한 클러스터면 1, 아니면 0을 갖는 hidden variable이다. GMM을 사용한 분류는 $x_{n}$이 주어졌을 때 $k$개의 $\gamma(z_{nk})$를 계산하여 가장 높은 값의 responsibility를 주는 Gaussian distribution을 찾는 과정이다.
GMM을 학습하여 모든 parameter $\theta = \{\pi, \mu, \Sigma \}$을 계산했다면 베이즈 정리를 이용하여 $\gamma(z_{nk})$를 다음과 같이 계산할 수 있다(자세한 과정은 여기 참고).
$$\gamma(z_{nk}) = p(z_{nk}=1|x_{n}) = \frac{p(z_{nk}=1)p(x_{n}|z_{nk}=1)}{\sum_{j=1}^{K}p(z_{nj}=1)p(x_{n}|z_{nj}=1)} = \frac{\pi_{k}N(x_{n}|\mu_{k}, \Sigma_{k})}{\sum_{j=1}^{K}\pi_{j}N(x_{n}|\mu_{j}, \Sigma_{j})}$$
위 식에서 $\pi_{k}, \ p(z_{nk}=1)$모두 $k$번째 Gaussian distribution이 선택될 확률을 의미하기 때문에 서로 치환 가능하다.
3) EM 알고리즘을 사용한 GMM 학습 과정
GMM은 주어진 데이터 $X = \{x_{1}, x_{2}, \cdots, x_{n}\}$에 대해 EM 알고리즘을 사용하여 parameter $\pi, \mu, \Sigma$를 추정한다. 이를 위해 log-likelihood $L(X;\theta)$를 아래와 같이 정의한다.
$$L(X;\theta) = \text{ln}p(X|\pi, \mu, \Sigma) = \text{ln}\left\{ \prod_{n=1}^{N}p(x_{n}|\pi, \mu, \Sigma) \right\} = \sum_{n=1}^{N}\text{ln}\left\{ \sum_{k=1}^{K}\pi_{k}N(x_{n}|\mu_{k}, \Sigma_{k}) \right\}$$
이 log-likelihood를 최대화하는 $\pi, \mu, \Sigma$를 찾으면 주어진 데이터 $X$를 가장 잘 설명하는 GMM를 구성할 수 있다. 이는 MLE(Maximum Likelihood Estimation) 추정법이며, $\mu, \Sigma$는 log-likelihood를 편미분하여 계산하고 $\pi$(mixing coefficient)는 라그랑주 승수 사용하여 다음과 같이 구할 수 있다(계산과정은 여기 참고).
- $\mu_{k} = \frac{\sum_{n=1}^{N}\gamma(z_{nk})x_{n}}{\gamma(z_{nk})}$
- $\Sigma_{k} = \frac{\sum_{n=1}^{N} \gamma(z_{nk}) (x_{n}-\mu_{k}) (x_{n}-\mu_{k})^{T}}{\sum_{n=1}^{N} \gamma(z_{nk})}$
- $\pi_{k} = \frac{1}{N}\sum_{n=1}^{N} \gamma(z_{nk})$
EM 알고리즘을 사용하여 아래 과정을 반복하여 parameter를 추정한다.
- 모든 parameter에 초기값을 할당한다(초기화).
- E step: 초기 parameter를 고정해두고 responsibility을 계산한다.
- M step: 계산된 responsibility을 사용하여 앞서 구한 parameter들의 MLE 추정값 식에 대입하여 각 parameter 값을 업데이트 한다.
- log-likelihood로 convergence를 평가한다.
Bishop 형님의 Pattern Recognition책에서 GMM에서의 EM 알고리즘 과정에 대해 아래와 같이 설명하고 있다.

참고로 EM(Expectaion Maximization) 알고리즘은 latent variable을 지닌 probabilistic model에서 MLE 해를 찾는 일반적인 방법이다.

2. GMM를 활용한 클러스터링
GMM과 K-Means의 큰 차이점은 hard clustering, soft clustering 여부이다. K-Means 계열은 데이터를 하나의 클러스터에만 포함시키기 때문에 확률(불확실성)으로 표현할 수 없다는 단점이 있다. 반면 GMM은 각 데이터가 얼만큼의 확률로 해당 클러스터에 속하는지를 알 수 있다.
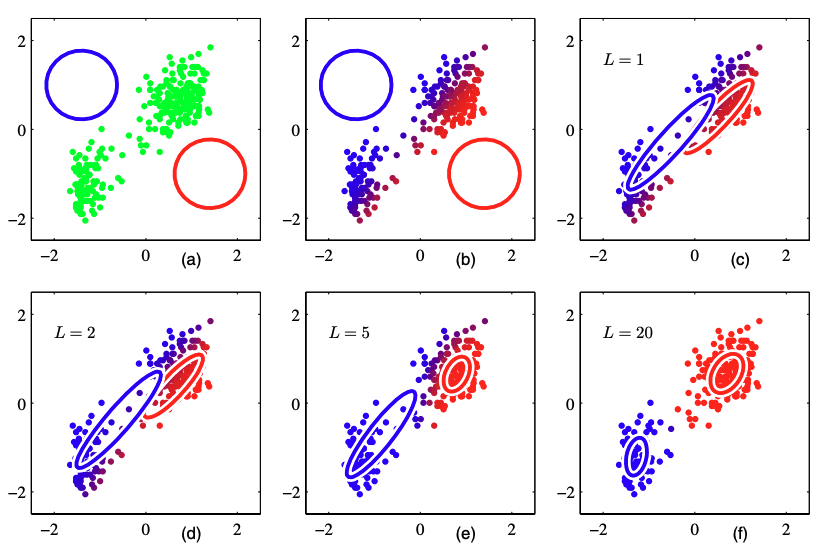
아래 그림은 Pattern Recognition 책에 있는 GMM(K=2) 학습 과정이다. a)는 데이터포인트들과 초기 Gaussian distribution가 위치해있다. b)는 초기값 상황에서 첫 E step을 통해 각 데이터에 대해서 responsibility를 계산한 결과이다. c)는 첫 M step을 통해 각 Gaussian distribution의 mean, covariance를 계산한 결과이다. d), e), f)는 각각 EM 알고리즘을 2번, 5번, 20번 반복한 결과이며 f)가 converge에 가까운 결과이다.
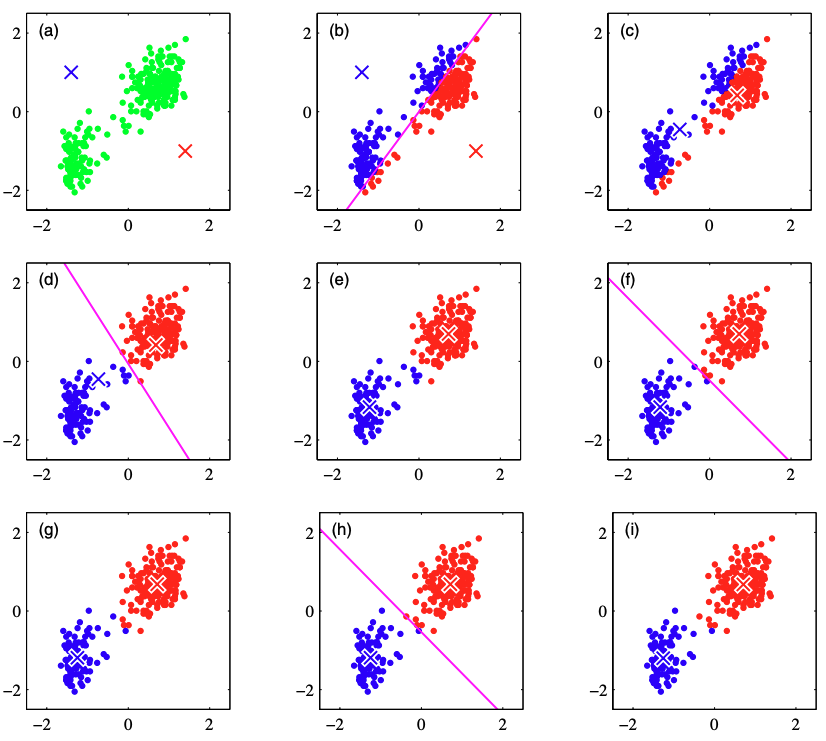
같은 데이터셋으로 K-Means로 클러스터링(K=2)하는 과정은 아래 그림과 같다. a)에서 데이터 포인트들과 초기 centroid $\mu_{1}, \mu_{2}$하고 b)에서 거리에 따라 각 데이터를 클러스터에 할당한다. c)에서 새롭게 centroid를 계산하고 이 과정으로 d)~i)까지 반복하여 최종적인 centroid와 클러스터를 생성한다.
'Pattern Recognition' 카테고리의 다른 글
| [ML] KL Divergence, Cross Entropy, Likelihood (0) | 2022.11.04 |
|---|---|
| 5. Density Estimation (0) | 2022.09.12 |
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| (참고) Gaussian Distribution (0) | 2022.08.06 |
