한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다.
0. Density Estimation
Density Estimation(밀도 추정)은 관찰된 데이터가 있을 때, 해당 데이터 분포에 내재된 확률밀도함수(probability density function)을 추정하는 방법이다(확률 함수가 아닌 확률밀도함수이다).
$$\begin{array}{}
f_{X}(x) \text{ is pdf}\\
P[a\le X\le b] = \int_{a}^{b}f_{X}(x)dx \\
\end{array}$$
대표적으로 Non-Parametric Density Estimation 방법인 Histogram, Kernel Density Estimation 등이 있다. 또한 Parametric Density Estimation으로는 GMM이 있다.
1. Histogram
Histogram은 데이터를 연속적인 간격(bin)으로 나누고 각 간격에서 관측된 표본의 빈도를 세고 그 값을 막대의 높이로 하여 데이터의 밀도로 표현한 그래프이다. 히스토그램의 시작점 값을 $x_{0}$, 폭 값(bin width)을 $h$라고 하면, 표본 데이터는 구간 $m$에 대하여 $[x_{0}+mh, \ x_{0}+(m+1)h]$에 존재하며, 데이터의 총 개수가 $n$일 때, 확률함수는 다음과 같이 정의한다.
$$P_{H}(x)= \frac{1}{n}\times \frac{Count(x)}{Width(x)} = \frac{Count(x)}{nh} $$
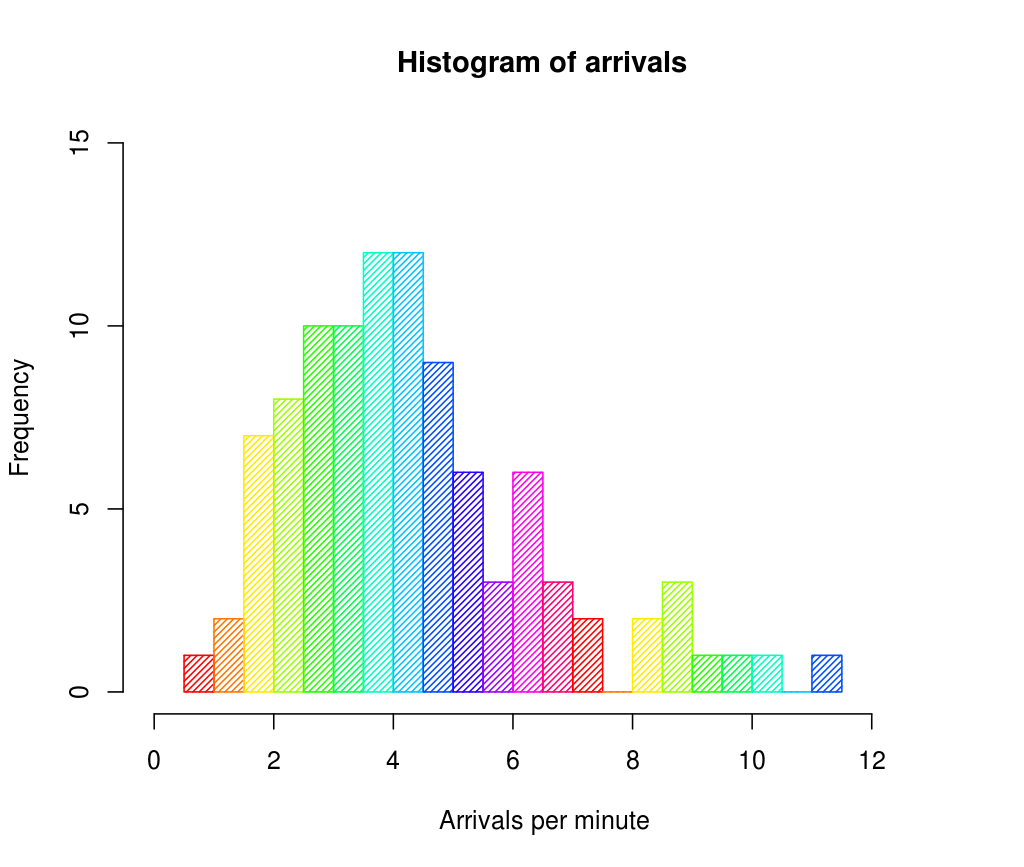
Histogram은 1,2차원의 데이터를 빠르게 시각화하는데 유용하다. 하지만 추정된 밀도가 불연속적이고 관측간격의 시작점(bin의 시작점)에 매우 의존적이며 feature차원이 증가할수록 관측구간(bin)의 수도 기하급수적으로 증거하는 차원의 저주의 등의 단점이 있다.
2. Kernel Density Estimation(커널 밀도 추정)
Kernel Density Estimation은 주어진 확률변수의 pdf를 추정하는 non-parametric한 방법이다. KDE는 Kernel을 사용하여 데이터 분포를 smoothing하고 pdf를 추정한다. 참고로 KDE는 다른 분야에서 Parzen-Rosenblatt window라고도 불린다.
1) Kernel이 무엇인가?
통계학에서 Kernel은 분야에 따라 몇 가지 다른 의미로 쓰인다(위키). 먼저 Bayesian statistics에서는 pdf, pmf 수식에서 domain variable을 제외한 형태를 의미한다. 아래 수식에서 분모의 $\sigma$가 제외된 이유는 domain variable $x$에 대한 함수가 아니기 때문이다.
$$\begin{array}{rcl}
\text{p.d.f} \ : & p(x|\mu, \sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \\
\text{kernel} \ : & p(x|\mu, \sigma^{2}) \propto e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}} \\
\end{array}
$$
반면 Non-parametric statistics에서 kernel은 weighting function을 의미하며 random variable의 density function을 추정하는 KDE 등에서 사용된다. 이때의 kernel은 non-negative real-valued integrable function이며 아래 두 조건을 만족해야 한다.
- Normalization: $\int_{-\infty }^{\infty}K(\mu)d\mu = 1$
- Symmetry: $K(-\mu) = K(\mu) \ \ \text{for all values of}\ \mu$
또한 kernel trick이라는 개념도 있는데 SVM등에서 사용되는 방식으로 자세한 내용은 여기에 잘 나와있다.
2) KDE
$< x_{1}, \cdots, x_{n} >$를 density function $f$에서 $\text{i.i.d}$로 샘플링된 데이터라고 하자. 이때 KDE를 통해 이 함수의 모양을 kernel을 사용하여 아래와 같이 추정할 수 있다.
$$\hat{f_{h}}(x) = \frac{1}{n}\sum_{i=1}^{n}K_{h}(x-x_{i}) = \frac{1}{nh}\sum_{i=1}^{n}K_{h}(\frac{x-x_{i}}{h})$$
$h$는 함수의 bandwidth 파라미터로 값이 작으면 kernel이 뾰족한 형태가되고 값이 크면 kernel이 완만한 형태가 된다. 위 수식은 다음과 같이 이해할 수 있다.
- 먼저 간측된 데이터 각각($x_{i}$)마다 해당 데이터 값을 중심으로 하는 kernel을 생성한다($K_{h}(x-x_{i})$)
- 만들어진 모든 kernel 함수들을 더하고 전체 데이터 개수로 나눈다.
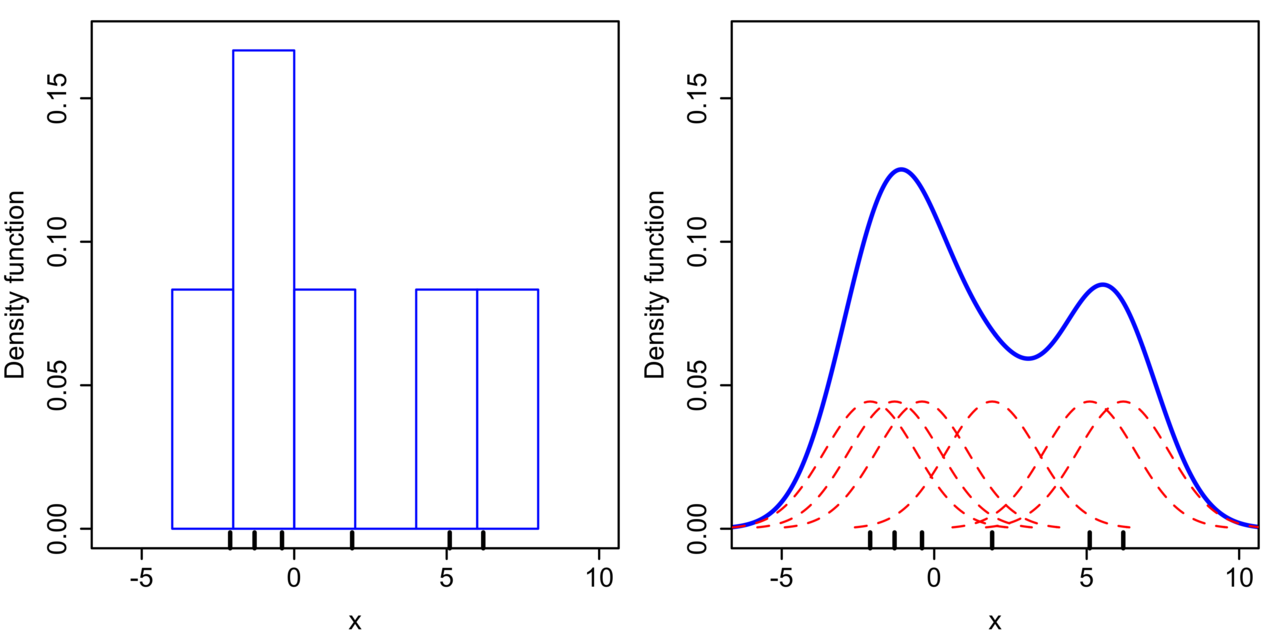
KDE는 kernel 함수 종류와 bandwidth $h$에 따라 모양이 크게 달라진다. 자주 사용되는 kernel 함수는 uniform, triangular, biweight, Epanechnikov, normal 분포 등이 있다.
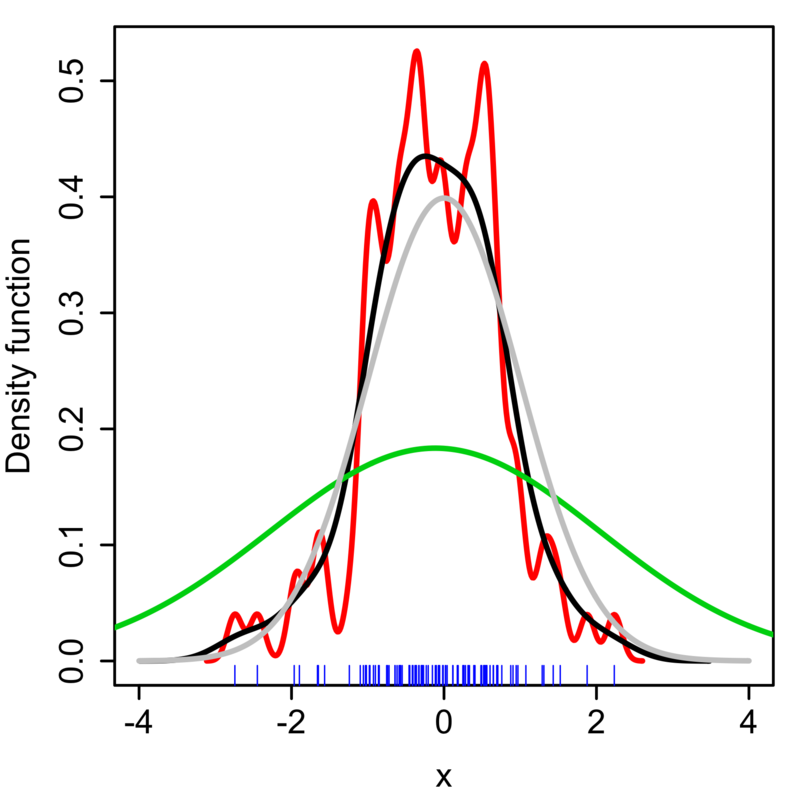
KDE로 적절한 estimation을 하기 위한 평가 방법으로는 MISE(Mean Integrated Squared Error)가 많이 사용된다.
$$\text{MISE}(h) = \text{E}\left[ \int (\hat{f_{h}}(x) - f(x) )^{2}dx \right]$$
적절한 bandwith $h$를 추정할 수도 있는데 만약 Gaussian kernel을 사용한다고 하면 $h$는 다음과 같은 값으로 사용하면 된다.
$$h = (\frac{4\hat{\sigma}^{5}}{3n})^{\frac{1}{5}}\approx 1.06\hat{\sigma}n^{-1/5}$$
[참고자료]
'Pattern Recognition' 카테고리의 다른 글
| [ML] KL Divergence, Cross Entropy, Likelihood (0) | 2022.11.04 |
|---|---|
| 4. Clustering (2) (2) | 2022.09.12 |
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| (참고) Gaussian Distribution (0) | 2022.08.06 |
