Language Model 등 분류해야할 class 개수가 매우 많을 때 softmax 계산에서 병목 현상이 발생할 수 있다. 이를 개선하기 위한 몇 가지 방법이 있는데 이를 정리하고자 한다.
1. 문제 정의
Huge Class 분류 문제는 크게 두 가지로 나눠볼 수 있다.
- single class 분류: 수 많은 class들 중 하나로 분류(ex. Language Model)
- multi class 분류: 수 많은 class들 중 1개 이상으로 분류
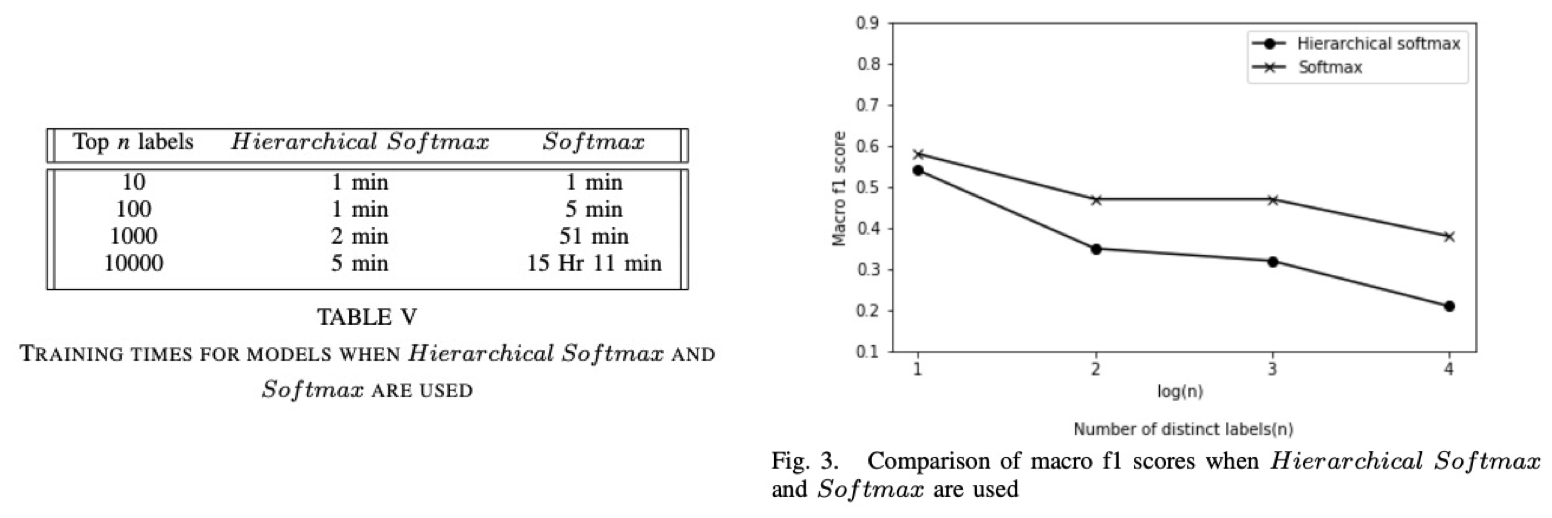
논문에 따르면 Huge Class 분류 모델을 학습 시킬 때 softmax 계산 비용이 커지고 성능이 떨어진다고 한다(출처: Effectiveness of Hierarchical Softmax in Large Scale Classification Tasks, 2019). 실제로 계산 비용은 class 수가 많아지면서 linear하게 증가한다.
2. 개선 방법
1) Candidate Sampling(출처)
꽤나 전통적인 방법으로 예측해야하는 label을 true target, 예측하지 않아야 하는 label들을 other target으로 보고 other target들에서 sampling하는 방식이다.
- Exhaustive Training: 모든 class들에 대해서 학습(기존 softmax 방식)
- Candidate Samling: sampling을 통해 set of candidate class를 얻고 학습
Candidate Sampling이 적용된 대표적인 방법은 Word2Vec을 학습시킬 때 주변 단어를 제외한 다른 단어들 중에서 sampling을 하여 학습시키는 방법이다. LM에 적용한다면 예측해야하는 다음 token을 제외한 다른 단어들 중 sampling하는 방식이다.
구체적으로는 다음과 같은 방식들이 있다.
i. Sampled Softmax
true target + sampling set from other target에 대해서 softmax를 계산하는 방식으로, 학습시에만 사용하고 평가 또는 추론 시 full-softmax를 계산한다.
ii. Noise Contrastive Estimation(NCE)
일반적으로 사용되는 likelihood maximization를 학습하는 것이 아니라, true data 1개 & noise sample $k$개를 sampling하여 candidate set을 구성한 후 binary cross-entropy로 true/noise를 구분하도록 학습시키는 방법니다.
2) Softmax Approximation
softmax 계산 방법에 변화를 주는 방식으로 데이터의 empirical distribution을 건들지 않기 때문에 좀더 안정적인 방법이라 생각한다.
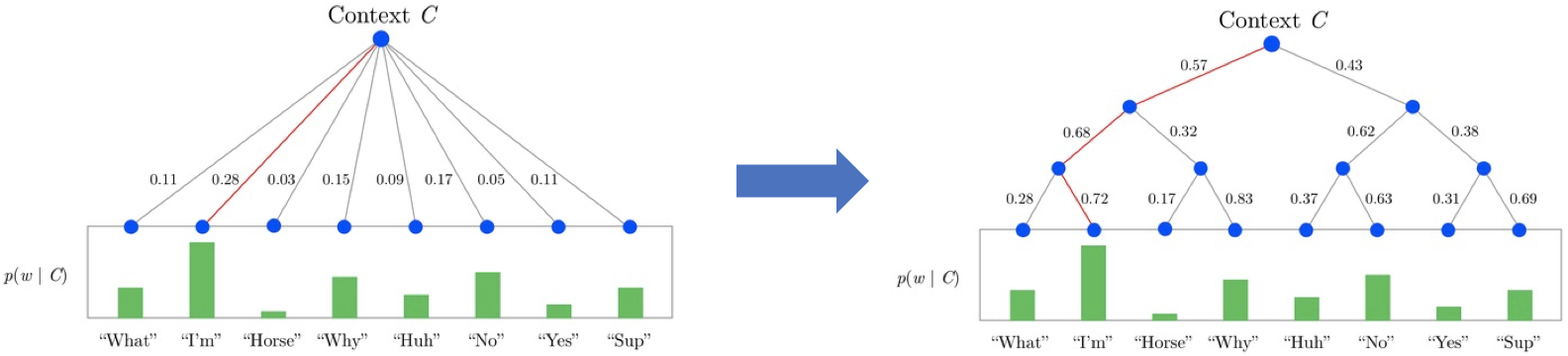
i. Hierarchical Softmax
이진 트리(binary tree)를 사용하여 단어에 대한 확률을 계산하는 방식으로 전체 계산 비용이 $O(C)$에서 $O(logC)$로 줄어든다.
ii. Differentiated Softmax(⭐︎)
제일 괜찮은 접근 방식이라는 생각이 드는 방법으로 Strategies for Training Large Vocabulary Neural Language Models(2015)라는 논문에서 제안되었다.
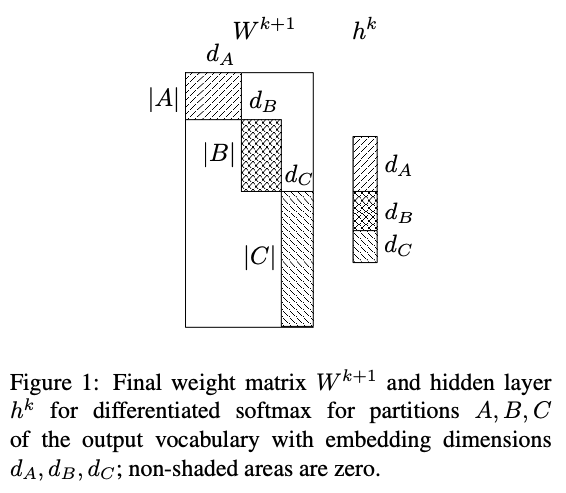
모델의 최종 hidden layer에서 softmax를 계산할 때 사용되는 weight matrix에서 class별로 동일한 차원의 embedding vector가 부여되어 있다. 이를 class 빈도수 기준으로 다른 차원의 embedding을 부여한다면, 해당 matrix의 gradient update시 모든 parameter가 아닌 일부 parameter만 업데이트 할 수 있다.
LM을 예로 들면 단어(token)별 빈도수 분포는 prior로 알 수 있으며, 이를 빈도수 별로 구간(partition)을 나눠놓는다. 이후 최종 hidden layer의 weight matrix에서 빈도수가 높은 단어에 대해서는 더 많은 embedding 차원을, 빈도수가 낮은 단어에 대해서는 더 적은 embedding 차원을 부여하여 softmax를 계산한다. 논문에서는 이러한 방법을 적용하여 학습&추론에서의 속도 개선 및 성능 향상을 얻을 수 있었다고 한다.
실제 데이터셋을 가지고 성능 측정을 해보고 싶었으나, 실험 환경에서 계속 cuda 에러가 나서 진행하지는 못했다. 구현 시 $h^{k}$ layer를 잘라 각각에 대해 hidden layer를 통과시키고($W^{k+1}$), 마지막에 concatenate한 다음 softmax를 계산해주면 될 듯 하다.
## softmax 모델
class SoftmaxModel(nn.Module):
def __init__(self, num_class, data_dim=32, hidden_dim=64):
super(SoftmaxModel, self).__init__()
self.fc1 = nn.Linear(data_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_class)
def forward(self, x, return_logits=False):
x = self.fc1(x)
x = self.fc2(x)
if return_logits:
return x
return F.softmax(x, dim=-1)
## Differentiated softmax 모델
class DifferentiatedSoftmaxModel(nn.Module):
def __init__(self, num_class, data_dim=32, hidden_dim=64, hidden_portions=[0.5,0.35,0], class_portions=[0.2, 0.3, 0]):
super(DifferentiatedSoftmaxModel, self).__init__()
self.fc1 = nn.Linear(data_dim, hidden_dim)
self.final_hiddens = [int(hidden_dim*portion) if portion != 0 else 0 for portion in hidden_portions ]
self.final_hiddens[-1] = hidden_dim - sum(self.final_hiddens[:-1])
self.class_bins = [int(num_class*portion) if portion != 0 else 0 for portion in class_portions ]
self.class_bins[-1] = num_class - sum(self.class_bins[:-1])
self.fc_finals = nn.ModuleList()
for final_hidden, class_bin in zip(self.final_hiddens, self.class_bins):
self.fc_finals.append(nn.Linear(final_hidden, class_bin))
def forward(self, x, return_logits=False):
x = self.fc1(x)
x_splitted = []
t = 0
for final_hidden in self.final_hiddens:
x_splitted.append( x[:, t:t+final_hidden] )
t += final_hidden
x = torch.cat([fc_final(x) for x, fc_final in zip(x_splitted, self.fc_finals)], dim=-1)
if return_logits:
return x
return F.softmax(x, dim=-1)
3. 결론
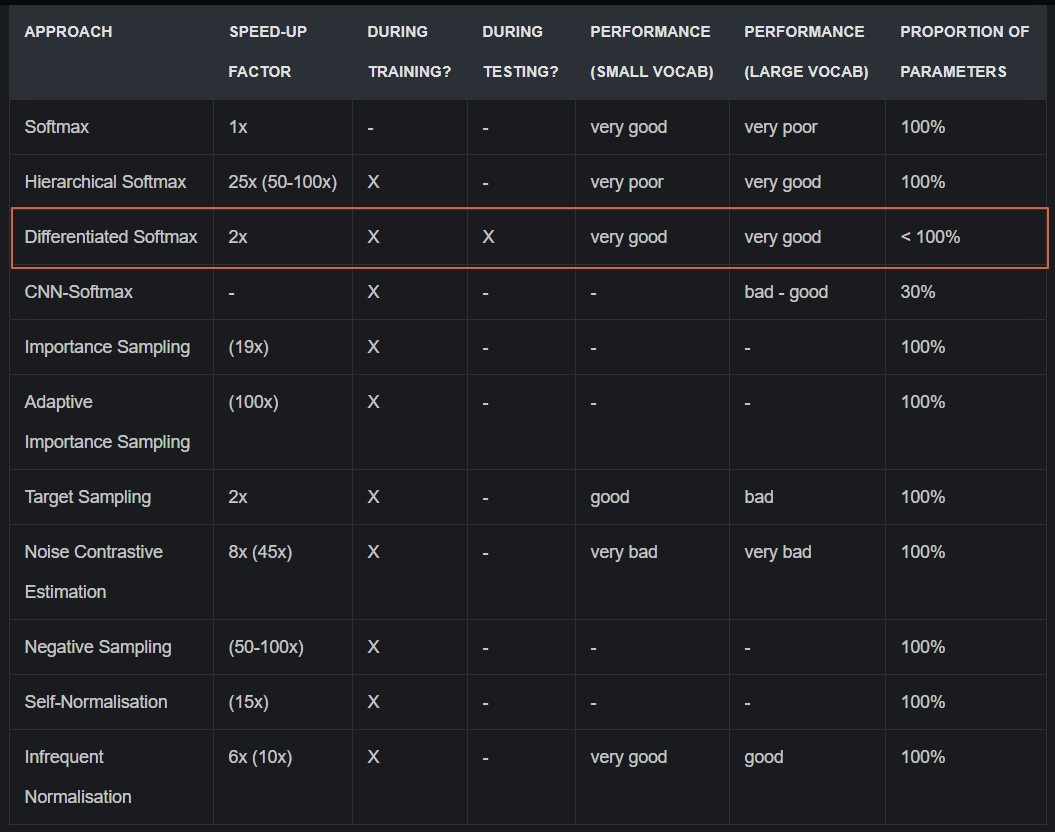
실제 실험결과에서는 Differentiated Softmax가 학습속도, 성능안정성에서 우위를 보였다고 한다. 실제 성능을 뽑아보진 않았지만 활용할 기회가 온다면 매우 테스트해보고 싶다.
'Toy Projects' 카테고리의 다른 글
| [LM] 언어모델 학습기 (0) | 2022.04.05 |
|---|---|
| [문서분류 PoC] Long Document & Class Imbalance (0) | 2021.05.20 |
| Selenium를 활용한 PAPAGO 번역 사용기 (0) | 2020.06.07 |
Language Model 등 분류해야할 class 개수가 매우 많을 때 softmax 계산에서 병목 현상이 발생할 수 있다. 이를 개선하기 위한 몇 가지 방법이 있는데 이를 정리하고자 한다.
1. 문제 정의
Huge Class 분류 문제는 크게 두 가지로 나눠볼 수 있다.
- single class 분류: 수 많은 class들 중 하나로 분류(ex. Language Model)
- multi class 분류: 수 많은 class들 중 1개 이상으로 분류
논문에 따르면 Huge Class 분류 모델을 학습 시킬 때 softmax 계산 비용이 커지고 성능이 떨어진다고 한다(출처: Effectiveness of Hierarchical Softmax in Large Scale Classification Tasks, 2019). 실제로 계산 비용은 class 수가 많아지면서 linear하게 증가한다.

2. 개선 방법
1) Candidate Sampling(출처)
꽤나 전통적인 방법으로 예측해야하는 label을 true target, 예측하지 않아야 하는 label들을 other target으로 보고 other target들에서 sampling하는 방식이다.
- Exhaustive Training: 모든 class들에 대해서 학습(기존 softmax 방식)
- Candidate Samling: sampling을 통해 set of candidate class를 얻고 학습
Candidate Sampling이 적용된 대표적인 방법은 Word2Vec을 학습시킬 때 주변 단어를 제외한 다른 단어들 중에서 sampling을 하여 학습시키는 방법이다. LM에 적용한다면 예측해야하는 다음 token을 제외한 다른 단어들 중 sampling하는 방식이다.
구체적으로는 다음과 같은 방식들이 있다.
i. Sampled Softmax
true target + sampling set from other target에 대해서 softmax를 계산하는 방식으로, 학습시에만 사용하고 평가 또는 추론 시 full-softmax를 계산한다.
ii. Noise Contrastive Estimation(NCE)
일반적으로 사용되는 likelihood maximization를 학습하는 것이 아니라, true data 1개 & noise sample
2) Softmax Approximation
softmax 계산 방법에 변화를 주는 방식으로 데이터의 empirical distribution을 건들지 않기 때문에 좀더 안정적인 방법이라 생각한다.
i. Hierarchical Softmax
이진 트리(binary tree)를 사용하여 단어에 대한 확률을 계산하는 방식으로 전체 계산 비용이

ii. Differentiated Softmax(⭐︎)
제일 괜찮은 접근 방식이라는 생각이 드는 방법으로 Strategies for Training Large Vocabulary Neural Language Models(2015)라는 논문에서 제안되었다.
모델의 최종 hidden layer에서 softmax를 계산할 때 사용되는 weight matrix에서 class별로 동일한 차원의 embedding vector가 부여되어 있다. 이를 class 빈도수 기준으로 다른 차원의 embedding을 부여한다면, 해당 matrix의 gradient update시 모든 parameter가 아닌 일부 parameter만 업데이트 할 수 있다.
LM을 예로 들면 단어(token)별 빈도수 분포는 prior로 알 수 있으며, 이를 빈도수 별로 구간(partition)을 나눠놓는다. 이후 최종 hidden layer의 weight matrix에서 빈도수가 높은 단어에 대해서는 더 많은 embedding 차원을, 빈도수가 낮은 단어에 대해서는 더 적은 embedding 차원을 부여하여 softmax를 계산한다. 논문에서는 이러한 방법을 적용하여 학습&추론에서의 속도 개선 및 성능 향상을 얻을 수 있었다고 한다.

실제 데이터셋을 가지고 성능 측정을 해보고 싶었으나, 실험 환경에서 계속 cuda 에러가 나서 진행하지는 못했다. 구현 시
## softmax 모델
class SoftmaxModel(nn.Module):
def __init__(self, num_class, data_dim=32, hidden_dim=64):
super(SoftmaxModel, self).__init__()
self.fc1 = nn.Linear(data_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_class)
def forward(self, x, return_logits=False):
x = self.fc1(x)
x = self.fc2(x)
if return_logits:
return x
return F.softmax(x, dim=-1)
## Differentiated softmax 모델
class DifferentiatedSoftmaxModel(nn.Module):
def __init__(self, num_class, data_dim=32, hidden_dim=64, hidden_portions=[0.5,0.35,0], class_portions=[0.2, 0.3, 0]):
super(DifferentiatedSoftmaxModel, self).__init__()
self.fc1 = nn.Linear(data_dim, hidden_dim)
self.final_hiddens = [int(hidden_dim*portion) if portion != 0 else 0 for portion in hidden_portions ]
self.final_hiddens[-1] = hidden_dim - sum(self.final_hiddens[:-1])
self.class_bins = [int(num_class*portion) if portion != 0 else 0 for portion in class_portions ]
self.class_bins[-1] = num_class - sum(self.class_bins[:-1])
self.fc_finals = nn.ModuleList()
for final_hidden, class_bin in zip(self.final_hiddens, self.class_bins):
self.fc_finals.append(nn.Linear(final_hidden, class_bin))
def forward(self, x, return_logits=False):
x = self.fc1(x)
x_splitted = []
t = 0
for final_hidden in self.final_hiddens:
x_splitted.append( x[:, t:t+final_hidden] )
t += final_hidden
x = torch.cat([fc_final(x) for x, fc_final in zip(x_splitted, self.fc_finals)], dim=-1)
if return_logits:
return x
return F.softmax(x, dim=-1)
3. 결론
실제 실험결과에서는 Differentiated Softmax가 학습속도, 성능안정성에서 우위를 보였다고 한다. 실제 성능을 뽑아보진 않았지만 활용할 기회가 온다면 매우 테스트해보고 싶다.

'Toy Projects' 카테고리의 다른 글
| [LM] 언어모델 학습기 (0) | 2022.04.05 |
|---|---|
| [문서분류 PoC] Long Document & Class Imbalance (0) | 2021.05.20 |
| Selenium를 활용한 PAPAGO 번역 사용기 (0) | 2020.06.07 |
