RoPE를 소개한 논문의 내용을 간단히 정리하고자 한다.
1. 논문 내용
RoPE 이전의 모델들은 대부분 absolute & additive한 poisition embedding을 사용했었다.
RoPE는 relative & multiplicative한 방식으로 position embedding을 계산한다.
다음과 같이 $\textbf{q}_{m}, \textbf{k}_{n}, \textbf{v}_{n}$($m,n$은 position을 의미)가 있다고 하자.
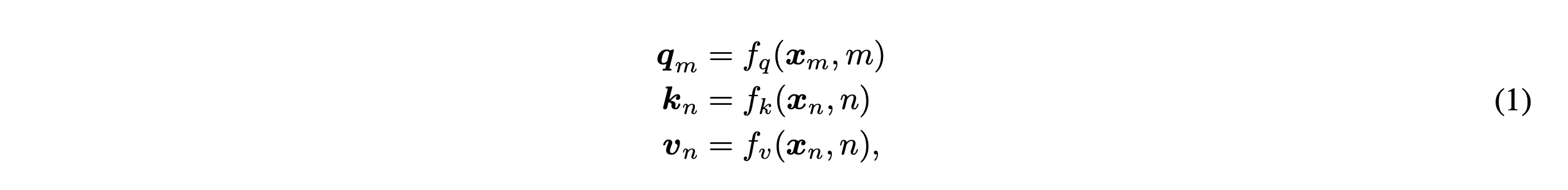
이때 attention은 다음과 같이 계산된다.

Absolute Position Embedding의 경우 (1)을 계산할 때 다음과 같이 position 정보를 embedding에 더한다.


Rotary Position Embedding이 목표로 하는 특징은 벡터 내적이 position $m,n$의 relative한 위치정보를 담도록 하는 것이다.

방법은 $\textbf{q}, \textbf{k}$ 벡터를 position에 따라 다른 각도로 회전하는 것이다.
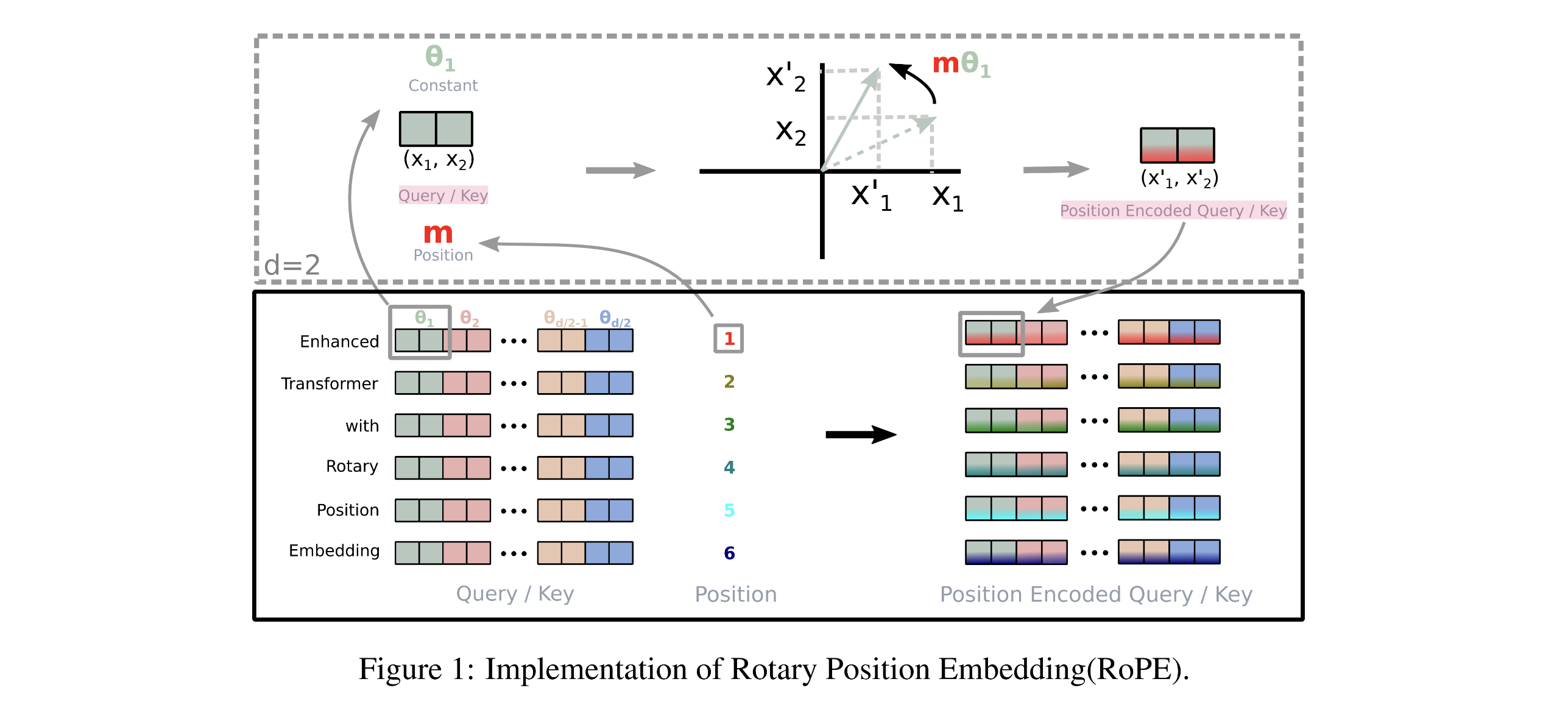
아래와 같이 2차원을 예시로 보자.

수식에서와 같이 $\textbf{x}_{m}, \textbf{x}_{n}$ 벡터를 rotary embedding을 해서 내적하면 $m-n$에 dependent한 내적값이 계산된다. 즉, 별도의 additive position embedding을 사용하지 않더라도 relative position embedding을 계산하게 되는 것이다.
2차원이 아닌 $d$ 차원으로 확장하면 다음과 같은 matrix 곱으로 표현할 수 있다.

$\textbf{q}, \textbf{k}$를 rotate시키는 것을 그림으로 표현하면 다음과 같다.
2. 그럼 구현은..?
수식 (15)의 matrix은 너무 sparse하기 때문에 논문 저자들은 다음과 같은 계산방식을 제안했다.($\otimes$는 vector outer product를 의미함)
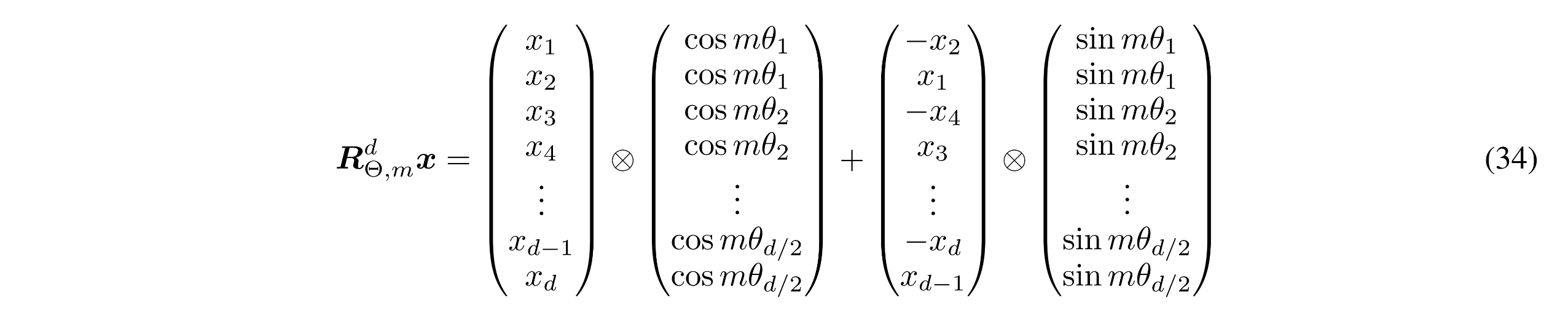
그리고 $\theta_{i}$를 다음과 같이 정의했다.

즉 RoPE는 position 정보 $\textbf{m}$과 $\theta$를 계산하기 위한 $\textbf{base}$를 사용한다.
구체적인 계산 과정은 여기에 기깔나게 정리되어 있다.
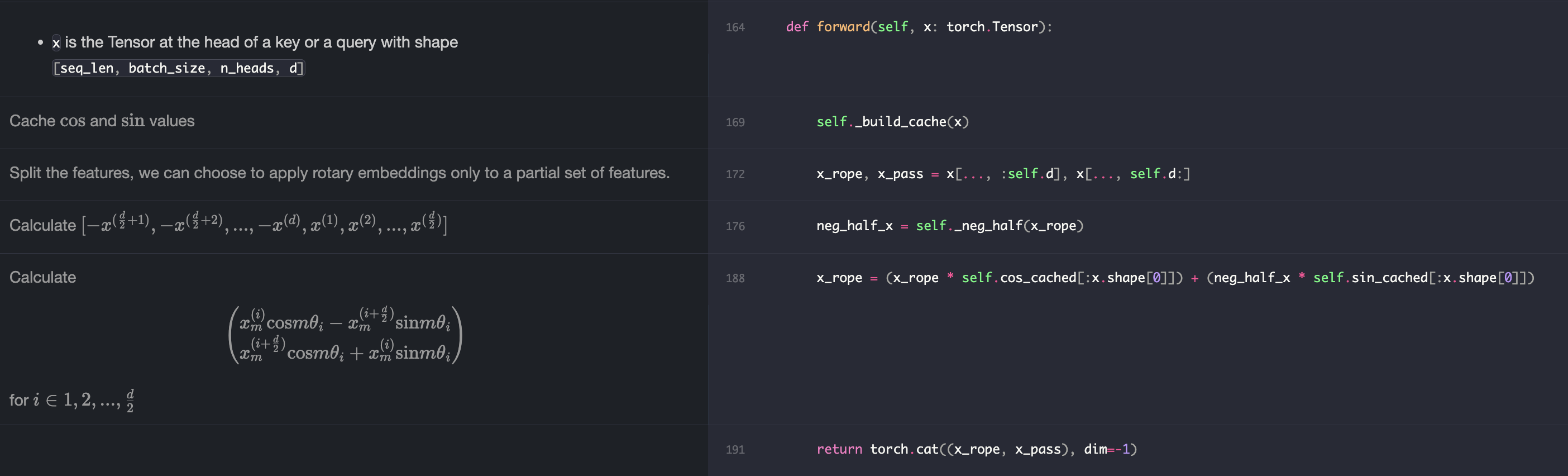
(1) 파라미터 세팅

(2) position vector, $\theta_{i}$, 회전변환을 위한 cos, sin 벡터 정의

(3) $\textbf{q}, \textbf{k}$를 rotary embedding을 적용하여 계산
[참고자료]
- https://arxiv.org/pdf/2104.09864
- https://nn.labml.ai/transformers/rope/index.html
- https://github.com/huggingface/transformers/blob/main/src/transformers/models/llama/modeling_llama.py
- https://github.com/abacusai/Long-Context/blob/main/python/models/interpolate.py
'논문 및 개념 정리' 카테고리의 다른 글
| [transformers] Scaled Dot Product Attention (0) | 2024.06.26 |
|---|---|
| Vector Outer Product (0) | 2024.06.26 |
| [2023] The Wisdom of Hindsight Makes Language Models Better Instruction Followers (1) | 2023.12.01 |
| Hold-out vs Cross-validation 차이 (0) | 2023.07.16 |
| Propensity Score (0) | 2023.06.28 |
RoPE를 소개한 논문의 내용을 간단히 정리하고자 한다.
1. 논문 내용
RoPE 이전의 모델들은 대부분 absolute & additive한 poisition embedding을 사용했었다.
RoPE는 relative & multiplicative한 방식으로 position embedding을 계산한다.
다음과 같이
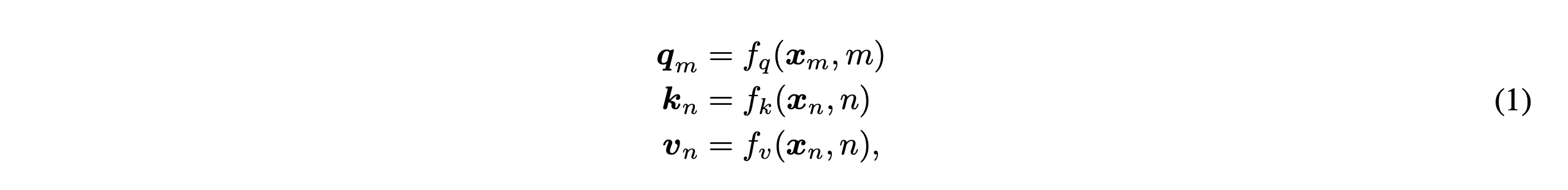
이때 attention은 다음과 같이 계산된다.

Absolute Position Embedding의 경우 (1)을 계산할 때 다음과 같이 position 정보를 embedding에 더한다.


Rotary Position Embedding이 목표로 하는 특징은 벡터 내적이 position

방법은
아래와 같이 2차원을 예시로 보자.

수식에서와 같이
2차원이 아닌


2. 그럼 구현은..?
수식 (15)의 matrix은 너무 sparse하기 때문에 논문 저자들은 다음과 같은 계산방식을 제안했다.(
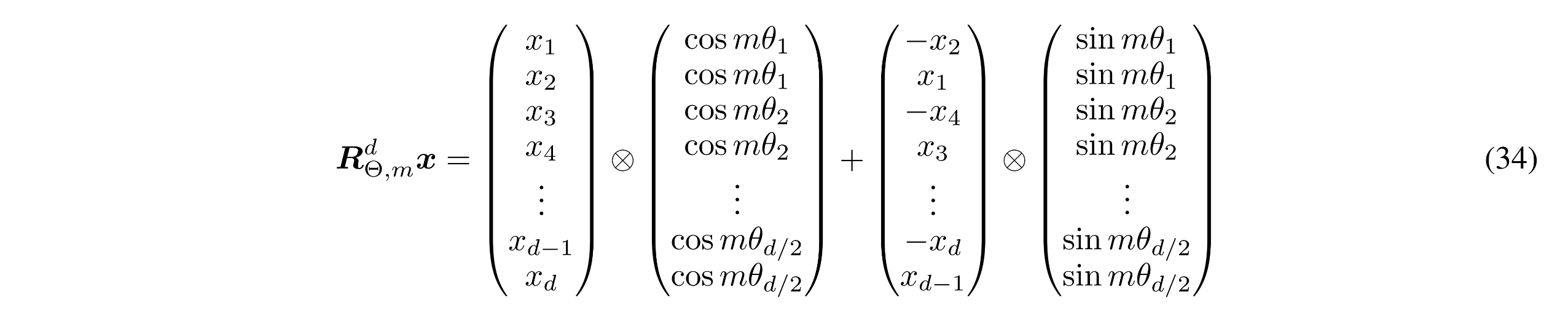
그리고

즉 RoPE는 position 정보
구체적인 계산 과정은 여기에 기깔나게 정리되어 있다.
(1) 파라미터 세팅

(2) position vector,

(3)

[참고자료]
- https://arxiv.org/pdf/2104.09864
- https://nn.labml.ai/transformers/rope/index.html
- https://github.com/huggingface/transformers/blob/main/src/transformers/models/llama/modeling_llama.py
- https://github.com/abacusai/Long-Context/blob/main/python/models/interpolate.py
'논문 및 개념 정리' 카테고리의 다른 글
| [transformers] Scaled Dot Product Attention (0) | 2024.06.26 |
|---|---|
| Vector Outer Product (0) | 2024.06.26 |
| [2023] The Wisdom of Hindsight Makes Language Models Better Instruction Followers (1) | 2023.12.01 |
| Hold-out vs Cross-validation 차이 (0) | 2023.07.16 |
| Propensity Score (0) | 2023.06.28 |
