한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다.
확률이론에서 기초가 되는 Gaussian Distribution에 대해 다뤄보고자 한다.
1. 단변량 가우시안(Univariate Gaussian)
- 단변량 가우시안 확률밀도 함수
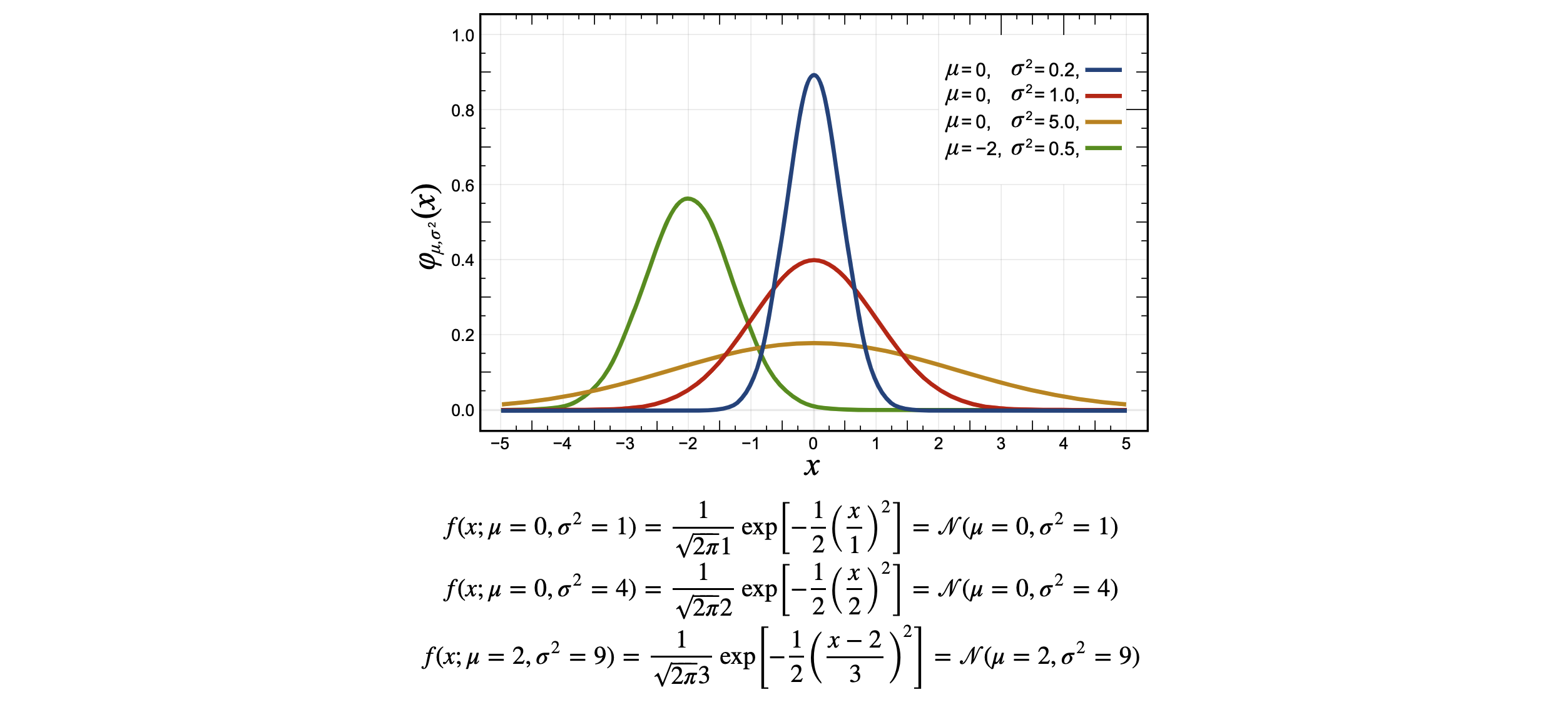
평균(기대값)을 $\mu$, 표준편차를 $\sigma$라고 할 때, Gaussian 분포는 다음과 같이 표현한다.
$$f(x) = N(\mu, \sigma) = \frac{1}{\sqrt[]{2\pi}\sigma}\text{exp}\left[ -\frac{1}{2}(\frac{x - \mu}{\sigma})^{2} \right]$$
2. 다변량 가우시안(Multivariate Gaussian)
- 다변량 가우시안 확률밀도 함수
D차원의 다변량 가우시안 정규분포(Multivariate Gaussian Normal Distribution, MVN)의 확률밀도함수는 평균 벡터 $\mu$와 공분산행렬 $\Sigma$라는 모수(parameter)를 가지며 다음과 같이 표현된다. MVN에서 공분산행렬은 일반적으로 양의 정부호 대칭행렬(positive definite symmetric matrix)만 다룬다.
$$N(x; \mu, \Sigma) = \frac{1}{(2\pi)^{D/2}\left| \Sigma \right|^{1/2}}\text{exp}\left[ -\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu) \right]$$
위 식에서 각 기호의 의미는 다음과 같다.
- $x \in R^{D}$: 확률 변수 벡터
- $\mu \in R^{D}$: 확률변수의 평균 벡터
- $\Sigma \in R^{D \times D}$: 공분산 행렬
- $\Sigma^{-1} = \Lambda \in R^{D \times D}$: 공분산행렬의 역행렬(정밀도 행렬(precision matrix)라고도 함)
- $\left| \Sigma \right| $: $\Sigma$의 determinant
- 다변량 가우시안 분포의 예
2차원을 예로 들면 확률변수가 $x = \left[
\begin{matrix}
x_{1} \\
x_{2} \\
\end{matrix}
\right] $ 평균과 공분산행렬이 각각 $\mu = \left[
\begin{matrix}
2 \\
3 \\
\end{matrix}
\right] ,
\Sigma = \left[
\begin{matrix}
1, 0 \\
0,1 \\
\end{matrix}
\right]$이라고 하면 가우시안 분포는 아래와 같다.
$$\left| \Sigma \right|=1, \Sigma^{-1} = \left[
\begin{matrix}
1, 0 \\
0,1 \\
\end{matrix}
\right]\\
(x-\mu)^{T}\Sigma^{-1}(x-u) = \left[ x_{1}-2, x_{2}-3 \right]\left[
\begin{matrix}
1, 0 \\
0,1 \\
\end{matrix}
\right]\left[
\begin{matrix}
x_{1}-2 \\
x_{2}-3 \\
\end{matrix}
\right] \\
N(x_{1}, x_{2}) = \frac{1}{2\pi}\text{exp}(-\frac{1}{2}((x_{1}-2)^{2}+(x_{2}-3)^{2}))$$
'Pattern Recognition' 카테고리의 다른 글
| 4. Clustering (2) (2) | 2022.09.12 |
|---|---|
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| 2. Random Variable & Probability Distribution (0) | 2022.08.05 |
| 1. Probability (0) | 2022.08.04 |
한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다.
확률이론에서 기초가 되는 Gaussian Distribution에 대해 다뤄보고자 한다.
1. 단변량 가우시안(Univariate Gaussian)
- 단변량 가우시안 확률밀도 함수
평균(기대값)을

2. 다변량 가우시안(Multivariate Gaussian)
- 다변량 가우시안 확률밀도 함수
D차원의 다변량 가우시안 정규분포(Multivariate Gaussian Normal Distribution, MVN)의 확률밀도함수는 평균 벡터
위 식에서 각 기호의 의미는 다음과 같다.
- 다변량 가우시안 분포의 예
2차원을 예로 들면 확률변수가
'Pattern Recognition' 카테고리의 다른 글
| 4. Clustering (2) (2) | 2022.09.12 |
|---|---|
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| 2. Random Variable & Probability Distribution (0) | 2022.08.05 |
| 1. Probability (0) | 2022.08.04 |
