한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다.
1. 통계 기초 및 확률 이론
Pattern recognition is the automated recognition of patterns and regularities in data(wikipedia)
패턴인식에서 통계학적인 기법들을 이용하여 데이터를 분석하고 확률기법들을 이용하여 데이터를 분류하거나 특성을 파악하는데 사용한다.
1) 통계용어
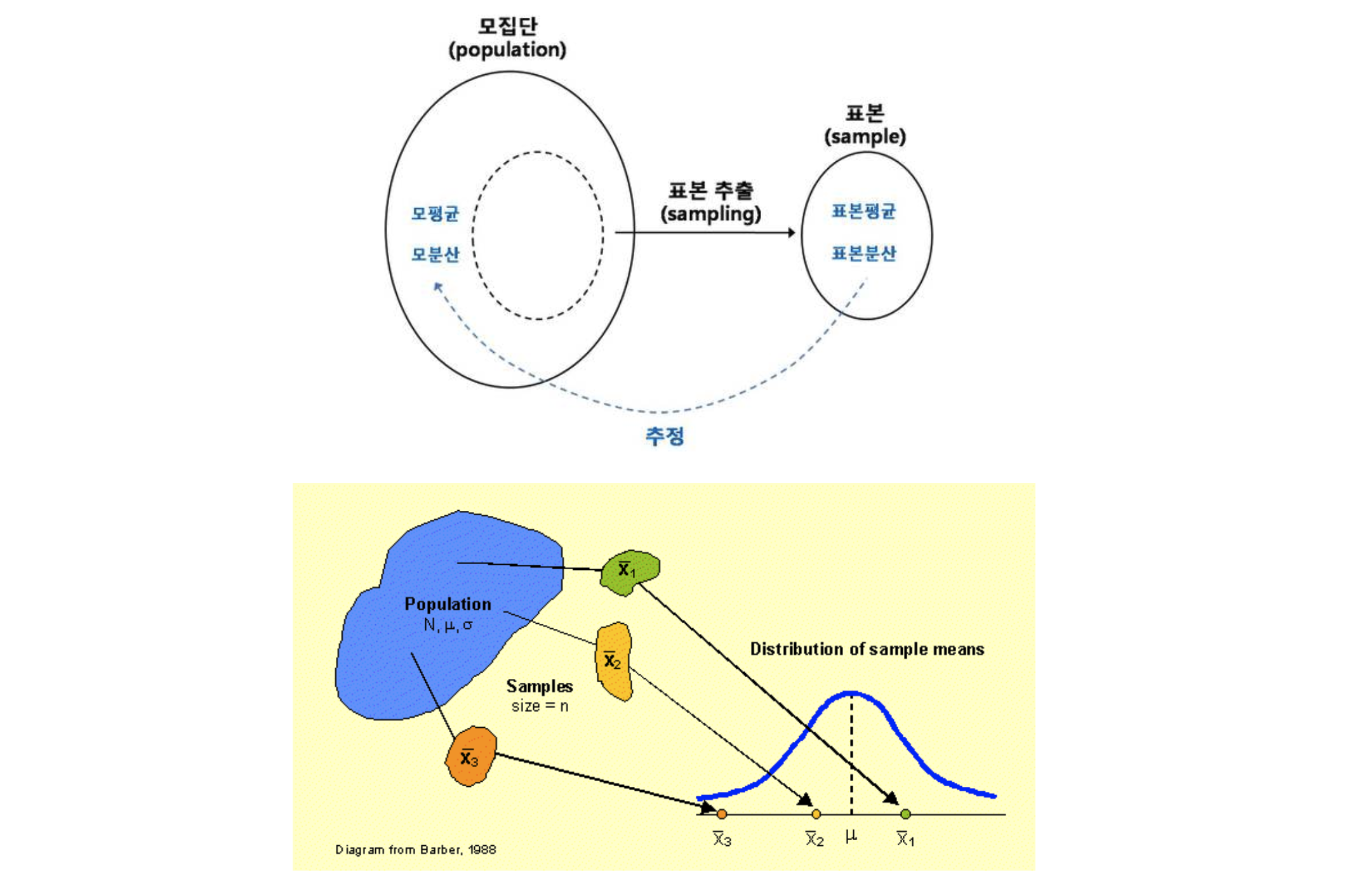
- 모집단(population): 데이터 분석의 관심이 되는 대상의 전체집합
- 표본(sample): 모집단의 부분집합으로 모집단의 특성을 파악하기 위해 수집된 개별 집단
- 표본 분포(sample distribution): 동일한 모집단에서 샘플링된 동일한 크기의 모든 가능한 표본으로부터 얻어진 통계값들의 분포
2) 모수(population parameter)와 통계량
모수(population parameter)는 모집단의 통계적인 특성치로 표본(sample)의 통계량을 가지고 모수를 추정하게 된다(참고). 아래는 꼭 알고있어야 할 통계량들이다.
- 평균(mean): 자료의 총합을 자료의 개수로 나눈 것으로 표본의 대표값을 계산하는 방법 중 하나
$$\overline{x} = \sum_{i=1}^{n} \frac{x_{i}}{n}$$
- 분산(variance): 데이터로부터 평균값의 차이에 대한 제곱 값의 평균으로, 자료가 얼마나 흩뿌려져 있는지를 나타냄
$$V = \sum_{i=1}^{n}\frac{(x_{i}-\overline{x})^{2}}{n}$$
- 표준편차(standart deviation): 분산은 제곱된 값이기 때문에 원래 단위와 달라지므로 분산에 제곱근을 취하여 데이터의 단위와 일치시킨 값
$$s = \sqrt{V} = \sqrt{\sum_{i=1}^{n}\frac{(x_{i}-\overline{x})^{2}}{n}}$$
- 공분산(covariance): 2개의 확률변수의 선형 관계를 나타내는 값으로, 각 변수가 변화하는 양상을 나타내는 통계적 척도이다. 예를 들어 만약 하나의 변수가 상승하는 경향을 보일 때 다른 값도 상승하는 선형 상관성이 있다면 양의 상관관계가 있다고 할 수 있다. 아래 식에서 $x=y$라면 분산으로 계산된다(참고자료: Visualizing covariance).
$$C(x,y) = \frac{1}{N}\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})$$
- 상관계수(correlation coefficient): 두 확률변수 $x,y$ 사이의 상관관계인 공분산을 정규화한 수치로 pearson correlation coefficient, Pearson's r 등으로도 불린다.
$$\rho_{xy} = \frac{C(x,y)}{s_{x}s_{y}}, \ -1 \le \rho \le 1$$
3) 확률 용어 정리
- 확률 실험(radom trial)
1) 같은 조건에서 반복 가능하며 2) 시행의 결과는 예측할 수 없으나, 모든 결과의 집합을 알 수 있으며 3) 시행을 반복할 때 각각의 결과는 불규칙하지만 반복의 수를 늘리면 규칙성이 나타나는 특징을 가진 실험을 확률실험이라고 한다.
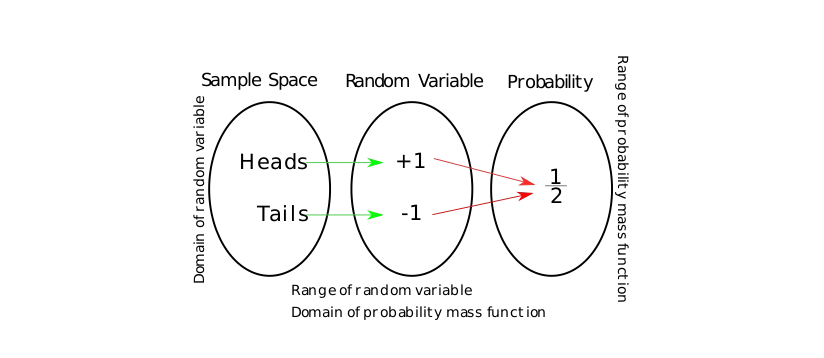
- 확률 변수(random variable)
랜덤하게 일어나는 확률 실험의 결과를 실수와 같은 measuarable space에 대응시켜주는 함수이다.
- 수학적 확률과 통계적 확률
수학적 확률은 표본공간 $S$의 각 근원 사건이 일어날 가능성이 동등하다고 가정하여 계산하는 확률을 의미한다(ex. 각 주사위 면이 나올 확률은 모두 $\frac{1}{6}$). 통계적 확률은 실제 현실에서의 사건에 대한 확률을 계산하는 방법으로 해당 사건이 발생한 도수를 전체 시행으로 나눈 상대도수로 추정한다.
- 표본 공간(sample space)과 확률 공간
어떤 이벤트에서 관찰할 일부를 지정 $\Rightarrow $ 일어날 수 있는 결과의 범위 정의 $\Rightarrow $ 해당 범위 내의 각 결과를 기호에 대응
확률 실험을 하는 과정은 위와 같은데, 이때 이를 통해 얻어진 기호화된 결과의 집합을 '표본 공간'이라고 한다. 그리고 표본 공간의 원소를 표본점, 표본 공간의 부분 집합을 사건, 오직 한 표본점으로 이루어진 사건을 근원사건, 표본 공간을 확률까지 대응시킨 결과의 집합이라 생각할 때의 공간을 '확률 공간'이라고 한다. 확률 공간은 확률 실험에서 가능한 모든 결과의 집합을 말한다.
- 주변 확률(marginal probability)
어떤 하나의 사건이 일어날 단순한 확률로 아무 조건이 붙지 않는 확률이다. 이 부분이 처음에는 헷갈렸었는데 여러 확률변수가 있을 때 단 하나의 확률 변수에 대한 확률을 말하는 것이다.
- 조건부 확률(conditional probability)
$A,B$ 두 개의 사건이 있을 때 $P(A|B)$는 "B가 일어났다고 가정할 때 A가 발생할 확률", "주어진 B에 대한 A의 확률"을 의미한다.
$$P(A|B) = \frac{P(A\cap B)}{P(B)}, \ P(B)>0$$
- 결합 확률(joint probability)
두 사건 $A,B$가 동시에 발생하는 확률로 조건부 확률로부터 수식이 유도된다.
$$P(A\cap B) = P(B)P(A|B) = P(A)P(B|A)$$
- 전체 확률 이론(law of total probability)
$B_{1}, B_{2}, \cdots, B_{N}$의 합집합이 표본 공간이며 서로 상호배타적(서로 독립)인 사건이라고 할때, 표본 공간 $S$의 분할 영역으로 이들 집합을 나타낼 수 있다.
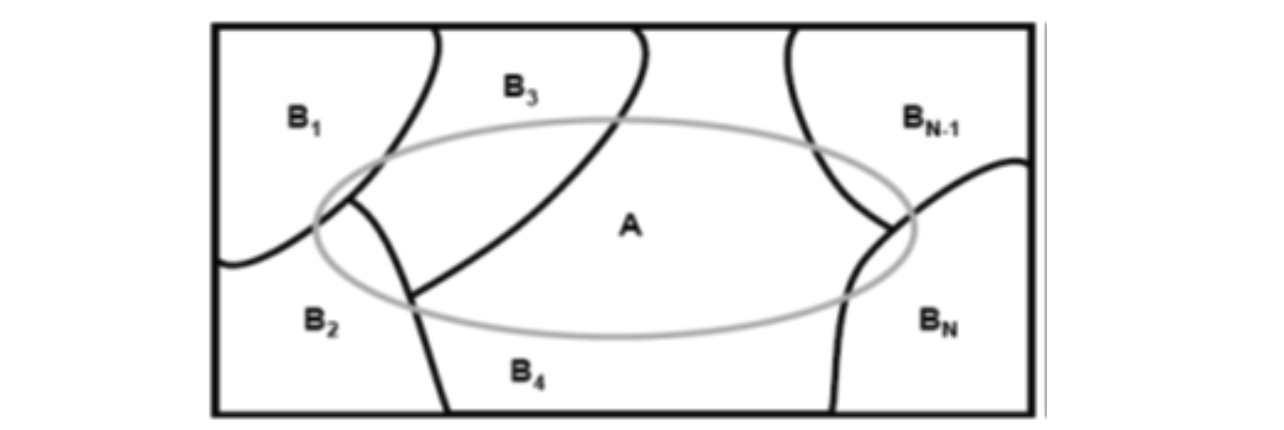
이 때, 사건 $A$는 다음과 같이 표현될 수 있다.
$$A = A\cap S = A \cap (B_{1}\cup B_{2} \cup \cdots \cup B_{N}) = (A \cap B_{1}) \cup ( A \cap B_{2}) \cup \cdots \cup (A \cap B_{N})$$
$B_{1}, B_{2}, \cdots, B_{N}$는 상호배타적이므로 조건부 확률을 이용하면 다음과 같이 각 사건 $B_{k}$에 대한 조건부 확률로 정의할 수 있다.
$$P(A) = P(A \cap B_{1}) + P(A \cap B_{2}) + \cdots + P(A \cap B_{N})$$
$$P(A) = P(A|B_{1})P(B_{1})+ \cdots + P(A|B_{N})P(B_{N}) = \sum_{k=1}^{N}P(A|B_{k})P(B_{k})$$
- 베이즈 정리(Bayes rule)
Bayes rule describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately (by conditioning it on their age) than simply assuming that the individual is typical of the population as a whole.
베이즈 정리는 어떤 사건이 서로 배반하는 원인 둘에 의해 일어난다고 할 때, 실제 사건이 일어났을 때 각 원인에 대한 확률을 구할 때 사용될 수 있다. $B_{1}, B_{2}, \cdots, B_{N}$의 합집합이 표본 공간 $S$인 경우, $A$사건이 일어났을 때 $B_{j}$사건이 일어날 확률은 다음과 같이 표현될 수 있다.
$$P(B_{j}|A) = \frac{P(A \cap B_{j})}{P(A)} = \frac{P(A|B_{j})P(B_{j})}{\sum_{k=1}^{N}P(A|B_{k})P(B_{k})}$$
패턴 분류 목적으로는 특정 샘플 $x$가 얻어졌을 때, 이것이 $w_{j}$ 클래스에서 나올 확률을 다음과 같이 구할 수 있다.
$$P(w_{j}|x) = \frac{P(x|w_{j})P(w_{j})}{P(x)} = \frac{P(x|w_{j})P(w_{j})}{\sum_{k=1}^{N}P(x|w_{k})P(w_{k})} $$
이때 각 요소는 다음과 같다이 정의된다.
- $P(w_{j})$: 클래스 $w_{j}$의 사전확률(prior probability)
- $P(w_{j}|x)$: 관측 $x$가 주어질 때 $w_{j}$에 대한 사후확률 (posterior probability)
- $P(x|w_{j})$: 클래스 $w_{j}$가 주어질 경우 관측 $x$가 일어날 조건부 확률 (우도, likelihood)
- $P(x)$: $x$가 일어날 확률로 결정에 영향을 미치지 않는 정규화 상수
$$P(w_{j}|x) = \frac{P(x|w_{j})P(w_{j})}{P(x)} = \frac{\text{likelihood}\times\text{prior probability}}{P(x)}$$
'Pattern Recognition' 카테고리의 다른 글
| 4. Clustering (2) (2) | 2022.09.12 |
|---|---|
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| (참고) Gaussian Distribution (0) | 2022.08.06 |
| 2. Random Variable & Probability Distribution (0) | 2022.08.05 |
한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다.
1. 통계 기초 및 확률 이론
Pattern recognition is the automated recognition of patterns and regularities in data(wikipedia)
패턴인식에서 통계학적인 기법들을 이용하여 데이터를 분석하고 확률기법들을 이용하여 데이터를 분류하거나 특성을 파악하는데 사용한다.
1) 통계용어
- 모집단(population): 데이터 분석의 관심이 되는 대상의 전체집합
- 표본(sample): 모집단의 부분집합으로 모집단의 특성을 파악하기 위해 수집된 개별 집단
- 표본 분포(sample distribution): 동일한 모집단에서 샘플링된 동일한 크기의 모든 가능한 표본으로부터 얻어진 통계값들의 분포

2) 모수(population parameter)와 통계량
모수(population parameter)는 모집단의 통계적인 특성치로 표본(sample)의 통계량을 가지고 모수를 추정하게 된다(참고). 아래는 꼭 알고있어야 할 통계량들이다.
- 평균(mean): 자료의 총합을 자료의 개수로 나눈 것으로 표본의 대표값을 계산하는 방법 중 하나
- 분산(variance): 데이터로부터 평균값의 차이에 대한 제곱 값의 평균으로, 자료가 얼마나 흩뿌려져 있는지를 나타냄
- 표준편차(standart deviation): 분산은 제곱된 값이기 때문에 원래 단위와 달라지므로 분산에 제곱근을 취하여 데이터의 단위와 일치시킨 값
- 공분산(covariance): 2개의 확률변수의 선형 관계를 나타내는 값으로, 각 변수가 변화하는 양상을 나타내는 통계적 척도이다. 예를 들어 만약 하나의 변수가 상승하는 경향을 보일 때 다른 값도 상승하는 선형 상관성이 있다면 양의 상관관계가 있다고 할 수 있다. 아래 식에서
- 상관계수(correlation coefficient): 두 확률변수
3) 확률 용어 정리
- 확률 실험(radom trial)
1) 같은 조건에서 반복 가능하며 2) 시행의 결과는 예측할 수 없으나, 모든 결과의 집합을 알 수 있으며 3) 시행을 반복할 때 각각의 결과는 불규칙하지만 반복의 수를 늘리면 규칙성이 나타나는 특징을 가진 실험을 확률실험이라고 한다.
- 확률 변수(random variable)
랜덤하게 일어나는 확률 실험의 결과를 실수와 같은 measuarable space에 대응시켜주는 함수이다.

- 수학적 확률과 통계적 확률
수학적 확률은 표본공간
- 표본 공간(sample space)과 확률 공간
어떤 이벤트에서 관찰할 일부를 지정
확률 실험을 하는 과정은 위와 같은데, 이때 이를 통해 얻어진 기호화된 결과의 집합을 '표본 공간'이라고 한다. 그리고 표본 공간의 원소를 표본점, 표본 공간의 부분 집합을 사건, 오직 한 표본점으로 이루어진 사건을 근원사건, 표본 공간을 확률까지 대응시킨 결과의 집합이라 생각할 때의 공간을 '확률 공간'이라고 한다. 확률 공간은 확률 실험에서 가능한 모든 결과의 집합을 말한다.
- 주변 확률(marginal probability)
어떤 하나의 사건이 일어날 단순한 확률로 아무 조건이 붙지 않는 확률이다. 이 부분이 처음에는 헷갈렸었는데 여러 확률변수가 있을 때 단 하나의 확률 변수에 대한 확률을 말하는 것이다.
- 조건부 확률(conditional probability)
- 결합 확률(joint probability)
두 사건
- 전체 확률 이론(law of total probability)

이 때, 사건
$B_{1}, B_{2}, \cdots, B_{N}
- 베이즈 정리(Bayes rule)
Bayes rule describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately (by conditioning it on their age) than simply assuming that the individual is typical of the population as a whole.
베이즈 정리는 어떤 사건이 서로 배반하는 원인 둘에 의해 일어난다고 할 때, 실제 사건이 일어났을 때 각 원인에 대한 확률을 구할 때 사용될 수 있다.
패턴 분류 목적으로는 특정 샘플
이때 각 요소는 다음과 같다이 정의된다.
'Pattern Recognition' 카테고리의 다른 글
| 4. Clustering (2) (2) | 2022.09.12 |
|---|---|
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| (참고) Gaussian Distribution (0) | 2022.08.06 |
| 2. Random Variable & Probability Distribution (0) | 2022.08.05 |
