한성대학교 지준교수님 강의자료를 통해 기초적인 개념들을 다지고자 한다.
1. 확률변수와 확률분포
- 확률변수란?
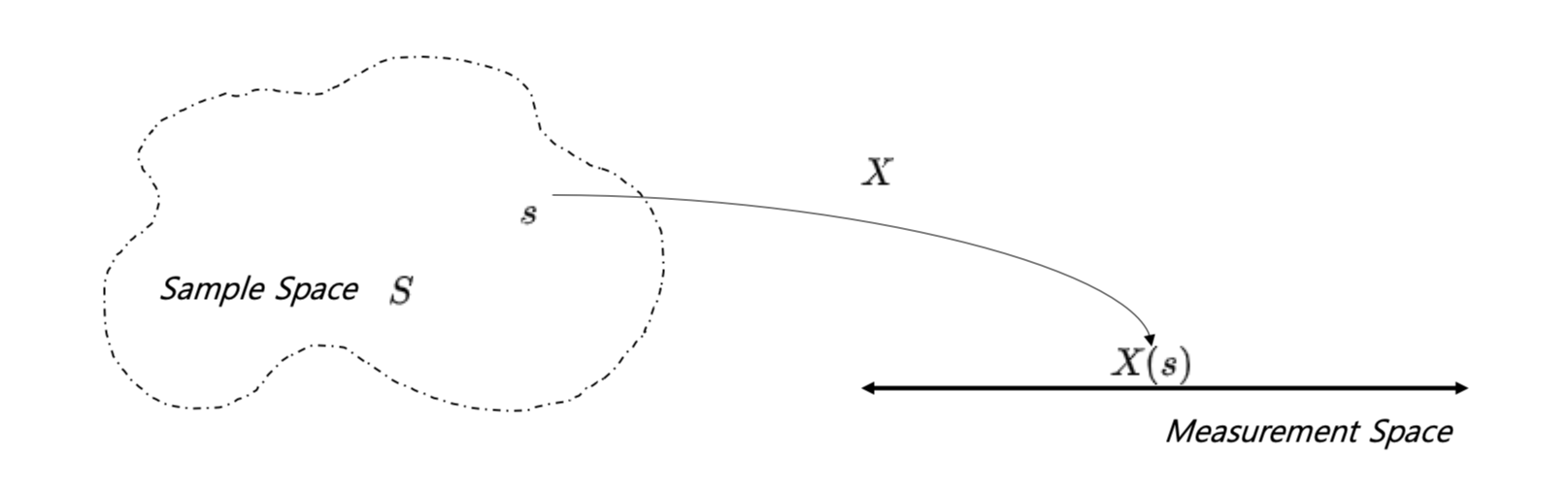
확률변수(random variable)란 확률실험에 따라 정의되는 표본공간 $S$의 모든 원소를 실수 값을 대응시키는 함수이다. 즉, 확률실험 시행 결과 각각은 확률변수에 의해 실수 값으로 표현될 수 있다. 확률변수의 종류는 주사위 굴리기와 같은 이산변수(discrete variable), 몸무게, 키와 같은 연속변수(continuous variable)가 있다.
$$X:S \rightarrow R, \ \text{that is For} \ s \in S, \ X(s) \in R$$
- 확률분포란?
확률분포는 수치로 대응된 확률변수의 개별 값들이 가지는 확률값의 분포이며, 확률변수가 취할 수 있는 값을 확률공간상에 대응시키는 함수를 '확률분포함수'라고 한다.
ex) 두 개의 동전을 던지는 확률 실험에서 앞면이 나오는 숫자의 확률분포

- 확률변수의 평균(기대값)
먼저 구분해 볼 개념은 표본(sample, 일반 데이터)의 성질들을 표본성질이라고 하며, 확률분포의 성질은 모델(또는 모집단) 성질이라고 한다. 따라서 표본과 모집단의 성질을 다음과 같이 구분한다.
| 평균 | 분산 | |
| 표본 | $\overline{x}$ | $s^{2}$ |
| 모집단 | $\mu$ | $\sigma^{2}$ |
어떤 표본이 있을 때 $n_{x}$를 $x$값을 갖는 자료점의 수라고 하면 상대도수를 $\frac{n_{x}}{n}$와 같이 표현할 수 있다. 이때 표본평균을 다음과 같이 표현할 수 있다.
$$\overline{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i} = \frac{1}{n}\sum_{allx}^{}n_{x}x = \sum_{allx}^{}x\frac{n_{x}}{n}$$
이산자료의 모집단의 경우, $n$값을 증가시키면 즉, 표본의 개수를 늘리면 $\frac{n_{x}}{n}$는 통계적 확률에 접근한다. 이때의 기대값(expectation)은 다음과 같이 표현되며, 이는 어떤 실험을 무수히 반복했을 때 예상되는 평균 값을 의미한다.
$$E[x] = \mu = \sum_{allx}^{}xp(x)$$
연속확률변수의 경우 다음과 같이 표현된다.
$$E[x] = \mu = \int_{-\infty}^{\infty}xf_{X}(x)dx$$
- 확률변수의 분산
이산형 자료 표본의 분산은 다음과 같다($\frac{n_{x}}{n}$는 상대도수를 의미).
$$s^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i} - \overline{x})^{2} = \sum_{allx}^{}(x_{i} - \overline{x})^{2}\frac{n_{x}}{n}$$
이산자료 모집단의 분산은 $n$ 값을 증가시키면 상대도수가 통계적 확률에 근사하게 되며 다음과 같이 표현할 수 있다.
$$\sigma^{2} = \sum_{allx}^{}(x-\mu)^{2}p(x)$$
연속형 자료 모집단의 분산은 다음과 같이 표현한다.
$$\text{Var}[X] = \text{E}[(X-\text{E}(X))^{2}] = \int_{-\infty}^{\infty}(x-\mu)^{2}f_{X}(x)dx$$
$$\text{std}[X] = \text{Var}[X]^{1/2}$$
참고로 분산은 다음과 같이도 표현할 수 있다.
$$\text{Var}(X) = \text{E}[X^{2}] - \text{E}[X]^2$$
1) 확률분포함수의 종류
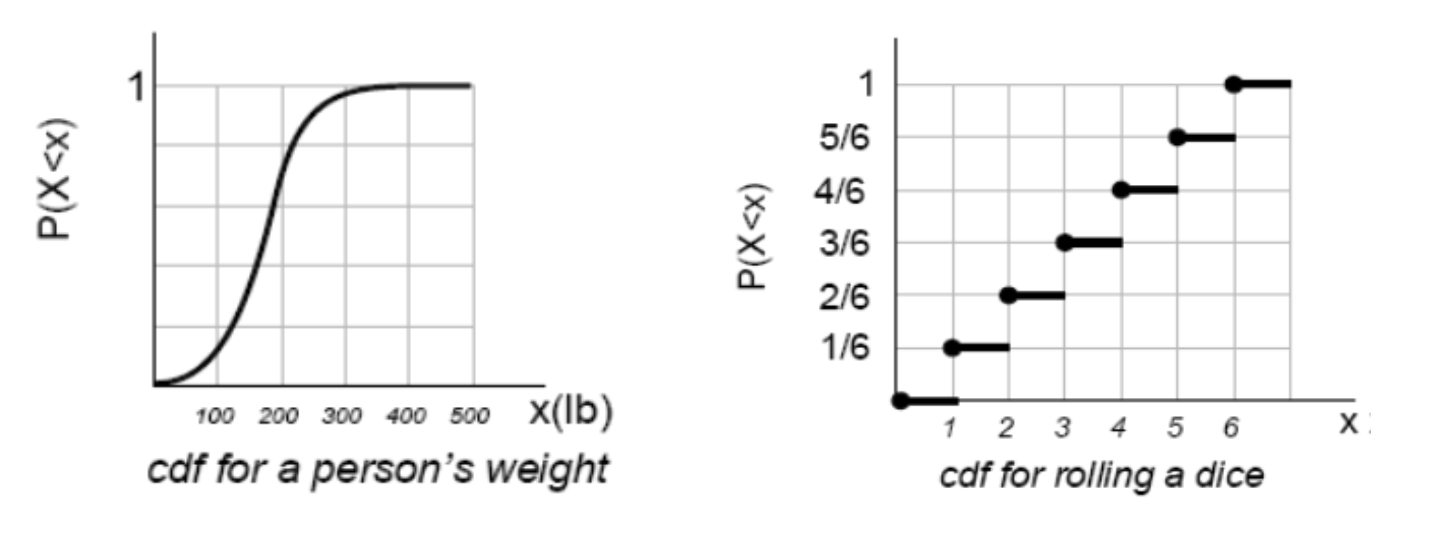
- 누적분포함수
확률변수 $X$의 누적분포함수(cumulative distribution function; cdf) $F_{X}(x)$는 확률변수 $X$가 $\{X \le x\}$일 확률함수이다.
$$F_{X}(x) = P(X \le x), \ \text{for} \ -\infty \lt x \lt \infty$$
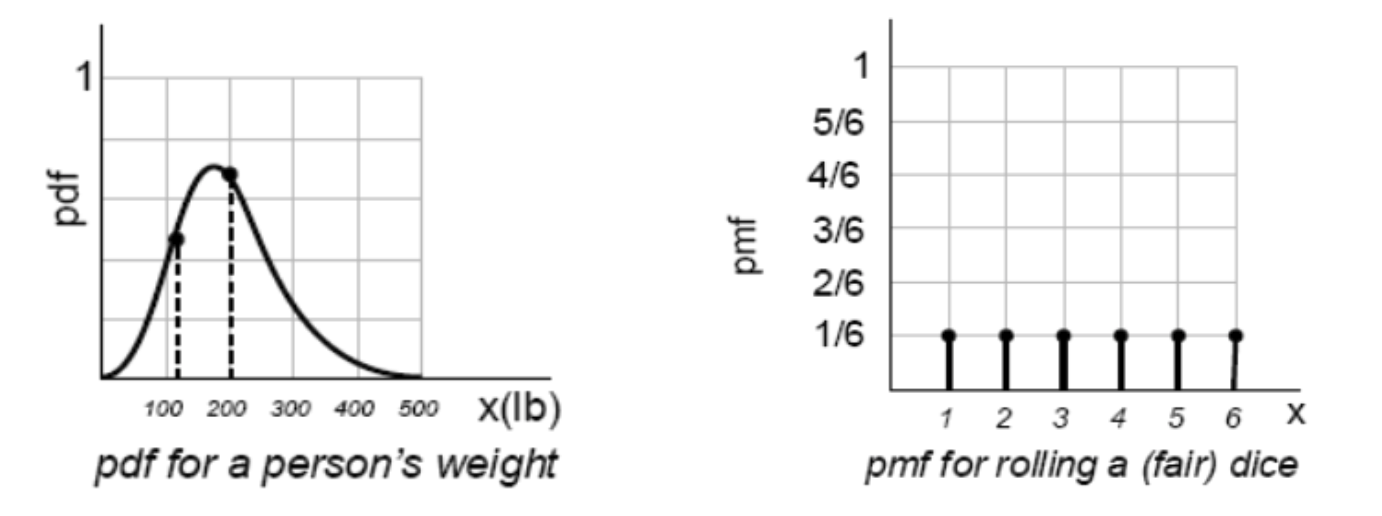
- 확률밀도함수
확률변수 $X$의 확률밀도함수(probability density function; pdf) $f_{X}(x)$는 연속확률변수 $X$의 누적분포 $F_{X}(x)$의 미분값으로 정의한다.
$$f_{X}(x) = \frac{dF_{X}(x)}{dX}$$
이산확률변수에서는 확률밀도함수와 동일한 개념으로 누적분포 $F_{X}(x)$의 차분값으로 정의하며, 이를 확률질량함수(probability mass function, pmf)라고 한다.
$$f_{X}(x) = \frac{\Delta F_{X}(x)}{\Delta X}$$
확률밀도함수는 다음과 같은 성질들이 있다.
- $f_{X}(x) \ge 0$
- P( a < X < b ) = \int_{a}^{b}f_{X}(x)dx
- $F_{X}(x) = \int_{-\infty}^{x}f_{X}(x)dx$
- $1 = \int_{-\infty}^{\infty}f_{X}(x)dx$
- $f_{X}(x|A) = \frac{d}{dx}F_{X}(x|A), \ \text{where} \ F_{X}(x|A) = \frac{P( \{X < x\} \cap A )}{P(A)}, \ \text{if} P(A)>0$
확률밀도함수는 확률의 밀도를 정의하는 것이므로, 실제 확률을 얻기 위해서는 확률밀도함수를 일정구간에서 적분해야한다. 반면에 확률질량함수는 실제 확률을 나타낸다.
2) 벡터 확률변수(다변수 확률변수)
- 벡터 확률변수란?
확률 변수가 2개 이상 존재하는 경우 확률변수의 개념을 확장하여 열(column) 벡터로 정의된다. 예를 들어, 학생들을 키와 몸무게로 표현한다면 확률변수가 2개가 되는 것이다(각 확률변수를 feature로 이해하면 좀 더 편하다). 확률변수가 2개인 경우 이중(binary) 랜덤변수라고 하며, 표본공간 $S$에 두 개의 확률변수 $X,Y$가 있을 때 각 표본값은 순서쌍 $(x,y)$으로 표현되는 새로운 표본공간(이를 결합 표본공간이라고 함)의 $xy$평면 상의 점에 대응된다. 그리고 누적분포함수, 확률밀도함수의 개념도 "결합 누적분포함수(joint cdf)"와 "결합 확률밀도함수(joint pdf)"로 확장된다.
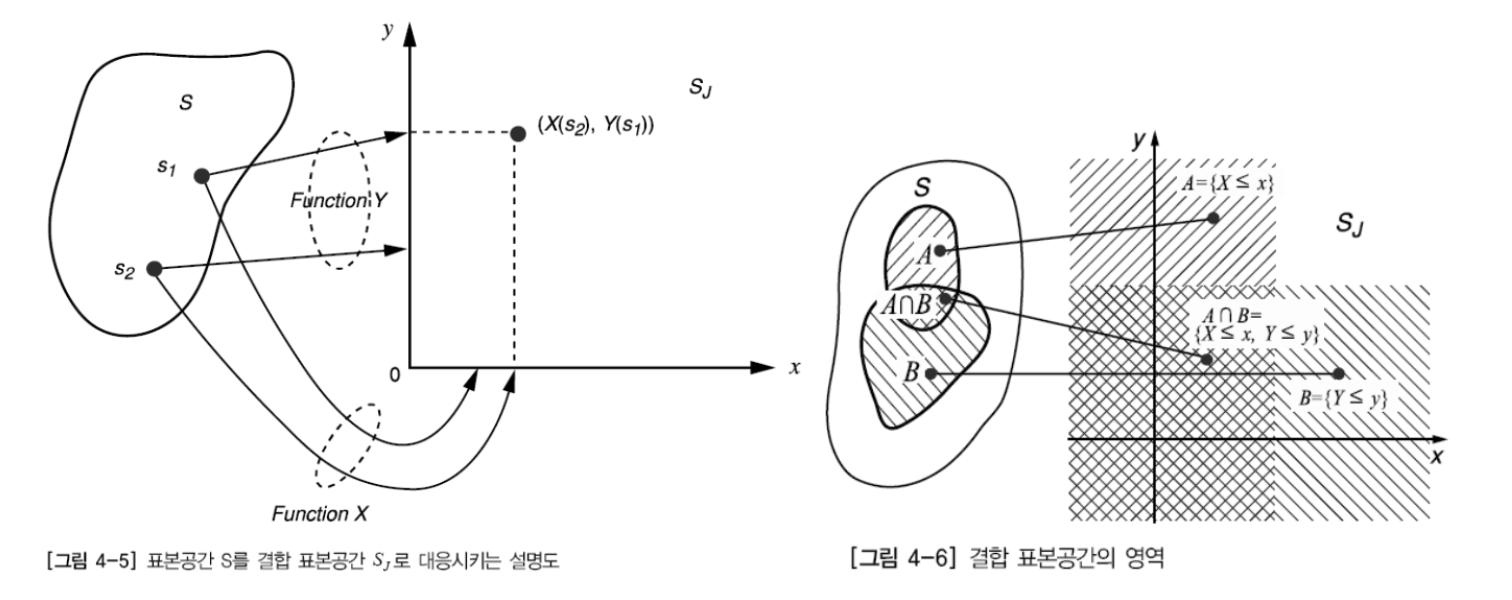
단일 확률변수의 누적 분포함수는 다음과 같다.
$$F_{X}(x) = P(X \le x), \ F_{Y}(y) = P(Y \le y)$$
이중(binary) 확률변수의 누적 분포함수는 다음과 같이 표현한다.
$$F_{X,Y}(x,y) = P(X \le x, Y \le y), \ P(X \le x, Y \le y) = P(A \cap B)$$
여러 확률변수로 구성된 랜덤 벡터 $X =[X_{1}, X_{2}, \cdots, X_{N}]^{T}$가 주어졌을때, 결합 누적분포함수(Joint Cumulative Density Function, joint cdf)는 다음과 같이 표현횐다.
$$F_{X}(x) = P_{X}[ \{X_{1} \le x_{1} \} \cap \{X_{2} \le x_{2} \} ] \cap \cdots \cap \{X_{1} \le x_{1} \} ]$$
그리고 결합 확률밀도함수(Joint Probability Density Function; Joint pdf)는 다음과 같이 표현된다.
$$f_{X}(x) = \frac{\delta ^{N}F_{X}(X)}{\delta x_{1}\delta x_{2}\cdots \delta x_{N}}$$
- 랜덤 벡터의 통계적 특징
변수가 1개인 확률변수에서 평균과 분산을 정의하듯이 2개 이상의 확률변수에서도 평균과 분산을 정의할 수 있다.
먼저 평균은 다음과 같이 평균벡터로 표현된다.
$$\mu = E[X] = [E[X_1], E[X_2], \cdots E[X_N]]^{T} = [\mu_1, \mu_2, \cdots, \mu_N]^{T}$$
다변수 확률변수에서 분산은 공분산행렬(Covariance Matrix)라고 하며, 다음과 같이 각 차원끼리의 공분산 값을 행렬로 표현한다.
$$\\ \Sigma = COV[X] = E[(X-\mu)(X-\mu)^{T}] \\
= \left[
\begin{array}{}
E[(x_1 - \mu_1)(x_1 - \mu_1)]&\cdots&E[(x_1 - \mu_1)(x_N - \mu_N)] \\
\vdots &\ddots &\vdots \\
E[(x_N - \mu_N)(x_1 - \mu_1)]&\cdots&E[(x_N - \mu_N)(x_N - \mu_N)] \\
\\
\end{array}
\right] = \left[
\begin{array}{}
\sigma_{1}^{2}&\cdots& c_{1N} \\
\vdots &\ddots &\vdots \\
c_{N1}&\cdots&\sigma_{N}^{2} \\
\\
\end{array}
\right]$$
공분산 행렬의 성질은 다음과 같다.
- $c_{ii} = \sigma_{i}^{2} = \text{Var}(X_{i})$
- $x_{i}$가 증가할 때 $x_{k}$가 증가한다면 $c_{ik} > 0$, $x_{k}$가 감소한다면 $c_{ik} < 0$
- 두 변수 $x_{i}, x_{k}$가 상관성이 없다면 $c_{ik} = 0$
- 상관계수
랜덤 벡터들로 생성된 행렬 $X$의 공분산 행렬은 다음과 같이 정의될 수 있다.
$$\Sigma = E[(X-\mu)(X-\mu)^{T}] = E[XX^{T}] - \mu E[X] - \mu E[X^{T}] + \mu \mu^{T} = S - \mu \mu^{T}$$
이때 S는 자기상관행렬로 다음과 같다.
$$S = E[XX^{T}] = \left[
\begin{array}{}
E[x_1x_1]&\cdots&E[x_1x_N] \\
\vdots&\ddots&\vdots \\
E[x_Nx_1]&\cdots&E[x_Nx_N] \\
\\
\end{array}
\right]$$
공분산행렬 $\Sigma$는 다음과 같이 상관행렬(correlation matrix)과 상관계수행렬과의 곱으로도 표현할 수 있다.
$$\Sigma = \Gamma R\Gamma = \left[
\begin{array}{}
\sigma_1&0&\cdots&0 \\
0 & \sigma_2 & & \\
\vdots& &\ddots&\vdots \\
0&\ & \cdots&\sigma_N \\
\\
\end{array}
\right] \left[
\begin{array}{}
1&\rho_{2}&\cdots&\rho_{1N} \\
\rho_{12} & 1 & & \\
\vdots& &\ddots&\vdots \\
\rho_{1N}&\ & \cdots&1 \\
\\
\end{array}
\right] \left[
\begin{array}{}
\sigma_1&0&\cdots&0 \\
0 & \sigma_2 & & \\
\vdots& &\ddots&\vdots \\
0&\ & \cdots&\sigma_N \\
\\
\end{array}
\right]$$
'Pattern Recognition' 카테고리의 다른 글
| 4. Clustering (2) (2) | 2022.09.12 |
|---|---|
| 4. Clustering (1) (0) | 2022.09.11 |
| 3. Maximum Likelihood Estimation(MLE) (0) | 2022.08.06 |
| (참고) Gaussian Distribution (0) | 2022.08.06 |
| 1. Probability (0) | 2022.08.04 |
