여러 이미지 관련 논문에서 baseline 모델로 사용되고 있는 ResNet 논문에 대해 정리하고자 한다(논문링크).
핵심 내용은 다음과 같다.
- Layer를 매우 많이 쌓을 때 특정 block 마다 입력을 layer 출력에 더해서 학습하면 더 잘된다
1. Introduction
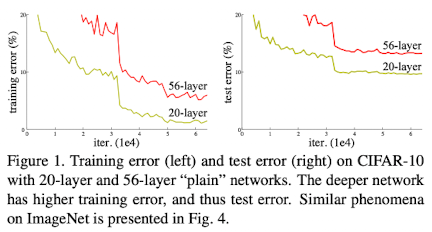
CNN의 layer 수를 증가시켜 deep하게 쌓으면 성능이 좋아질 것이라 예상됐지만 실제로는 위 그림처럼 train, test error 모두 증가하고 vanishing/exploding gradient 문제가 발생한다. 또한 deep 해지면 모델이 수렴은 했지만 성능이 나빠지는 degradation 문제가 발생한다.
본 연구에서는 이러한 문제들을 해결하는 deep residual learning에 대해 소개한다. Residual network는 layer을 단순하게 많이 쌓는 방식에 비해 optimize가 잘되고 성능이 좋은 장점이 있다.
2. Deep Residual Learning
먼저 논문에서 사용된 용어에 대해서 정리하면 아래와 같다.
- $\textbf{x}$: 각 block 단위에서의 입력
- $\mathcal{H}(\textbf{x})$: 각 block 단위에서 기대되는 개념적 결과(underlying mapping)
- $\mathcal{F}(\textbf{x})$: 각 block 단위에서의 실제 출력
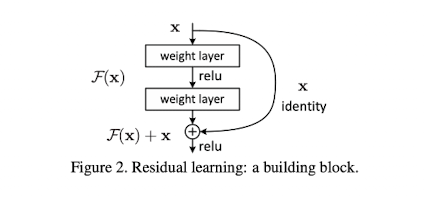
ResNet 논문에서는 block 단위에서 입력 $\textbf{x}$를 출력 $\mathcal{F}(\textbf{x})$에 더해줌으로써 stacked nonlinear layers가 $\mathcal{F}(\textbf{x}) := \mathcal{H}(\textbf{x}) - \textbf{x}$를 학습하는 방법을 제시하였다. 저자들은 이러한 residual mapping($\mathcal{H}(\textbf{x}) - \textbf{x}$)이 원래의 mapping($\mathcal{H}(\textbf{x})$)을 학습한 것 보다 더 쉬운 문제라는 가정을 한다.
각 building block은 아래 수식에서 (1)과 같이 정의할 수 있으며, dimension이 다를 시 linear projection을 추가하여 (2)와 같이도 사용할 수 있다.
$$\begin{array}{rcl}
\textbf{y} = \mathcal{F}(\textbf{x}, \{W_{i}\})+\textbf{x} & \cdots & (1) \\
\textbf{y} = \mathcal{F}(\textbf{x}, \{W_{i}\})+W_{s}\textbf{x} & \cdots & (2)
\end{array}$$
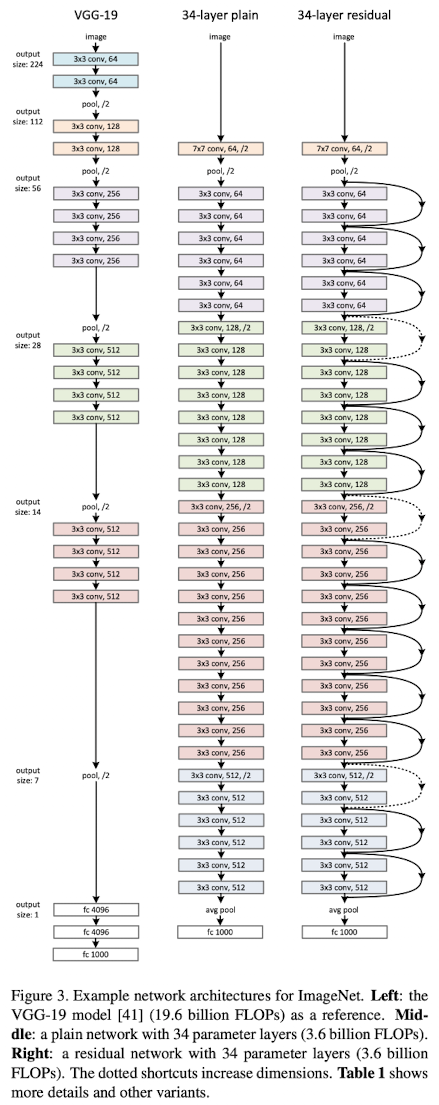
ResNet 모델은 아래 그림에서 맨 오른쪽 모델이며, 특정 layer 마다 입력을 출력에 더하는 형태로 구성된다.
3. Experiments
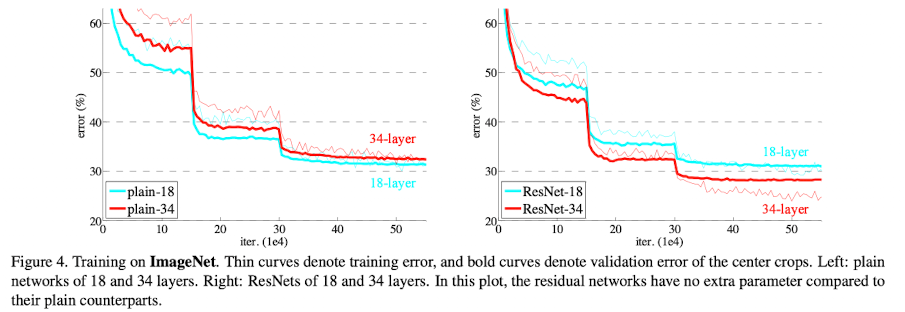
ResNet 방법을 사용하면 위 그래프에서처럼 layer를 증가시켜도 train error가 감소하는 것을 확인할 수 있다.
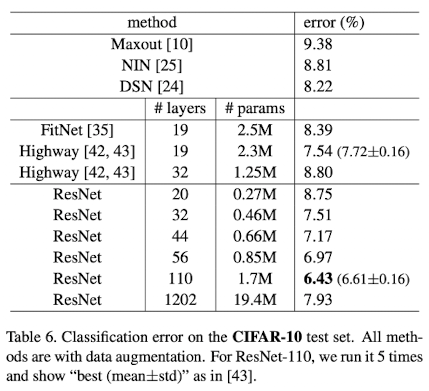
또한 다른 방법들에 비해 error rate이 낮다.
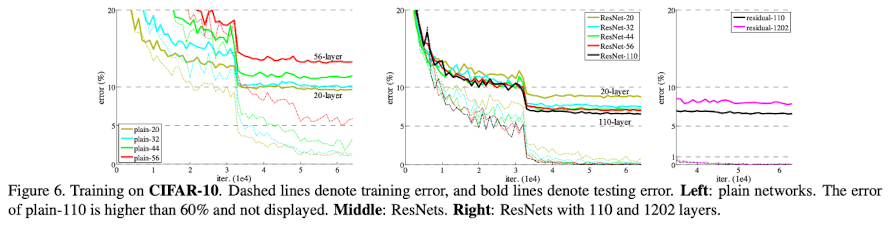
모델을 매우 키워서 1200 layer로도 실험한 결과 optimize가 매우 잘 되고 있는 것을 볼 수 있다. 다만 classification 성능이 안좋은 이유는 overfitting이 발생했기 때문이다.
4. 왜 잘될까?
ResNet이 잘 되는 이유는 명확하게 밝혀진 것 같지는 않다. 다만 많은 사람들이 주장하는 내용은 ensemble 효과가 있다는 것이다.
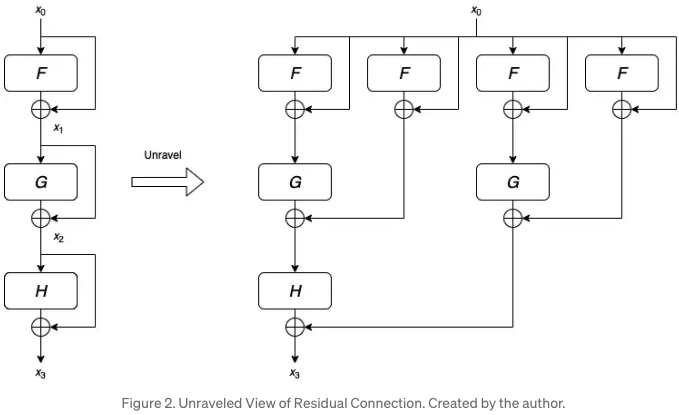
이 블로그글에 따르면 위 그림(unraveled view)처럼 입력을 더하면 layer가 깊어지면서 같은 입력을 여러번 학습한다고 한다. 수식적으로도 다음과 같이 표현할 수 있다.
$$\begin{array}{rcl}
x_{3} & = & H(x_{2})+x_{2} \\
& = & H[G(x_{1})+x_{1}] + G(x_{1})+x_{1} \\
& = & H[G[F(x_{0})+x_{0}]+F(x_{0})+x_{0}] + G[F(x_{0})+x_{0}]+F(x_{0})+x_{0}
\end{array}$$
